题目内容
17.已知点A、B在半径为1的⊙O上,直线AC与⊙O相切,OC⊥OB,连接AB交OC于点D.(Ⅰ)如图①,若∠OCA=60°,求OD的长;
(Ⅱ)如图②,OC与⊙O交于点E,若BE∥OA,求OD的长.
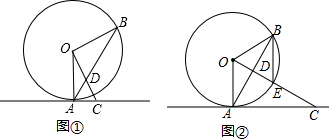
分析 (1)由切线的性质可知∠OAC=90°,由三角形的内角和定理可知∠AOC=30°,由∠AOB=∠AOC+∠BOC可得出∠AOB的度数,结合OA=OB可得出∠OAB=∠OBA=30°,由此可得出OD=AD,由∠OAB与∠DAC互余可知∠DAC=60°=∠DCA,由此得出△DAC为等边三角形,从而得出OD=AC,由特殊角的三角函数值即可得出结论;
(2)由OC⊥OB且OC=OB可知∠OBE=∠OEB=45°,再由BE∥OA可得出∠AOC=45°,结合切线性质可得出OA=AC,根据角与角之间的关系逐步得出∠CAD=∠CDA=67.5°,由此可得出AC=CD,结合勾股定理即可得出结论.
解答 解:(1)∵AC与⊙O相切,
∴∠OAC=90°.
∵∠OCA=60°,
∴∠AOC=30°.
∵OC⊥OB,
∴∠AOB=∠AOC+∠BOC=120°.
∵OA=OB,
∴∠OAB=∠OBA=30°,
∴OD=AD,∠DAC=60°
∴AD=CD=AC.
∵OA=1,
∴OD=AC=OA•tan∠AOC=$\frac{\sqrt{3}}{3}$.
(2)∵OC⊥OB,
∴∠OBE=∠OEB=45°.
∵BE∥OA,
∴∠AOC=45°,∠ABE=∠OAB,
∴OA=AC,∠OAB=∠OBA=22.5°,
∴∠ADC=∠AOC+∠OAB=67.5°.
∵∠DAC=90°-∠OAB=67.5°=∠ADC,
∴AC=CD.
∵OC=$\frac{AC}{sin∠AOC}$=$\sqrt{2}$,
∴OD=OC-CD=$\sqrt{2}$-1.
点评 本题考查了切线的性质、角的计算、等腰三角形的判定及性质、勾股定理以及特殊角的三角函数值,解题的关键是:(1)通过边角关系找出OD=AC;(2)通过边角关系找出AC=CD.本题属于基础题,难度不大,解决该题型题目时,根据角的计算找出相等的角,再由相等的角得出相等的边.

| A. | $\frac{2}{3}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{6}$ |
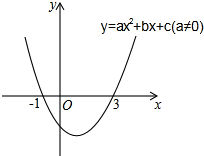 二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列说法:①2a+b=0,②当-1≤x≤3时,y<0;③3a+c=0;④若(x1,y1)(x2、y2)在函数图象上,当0<x1<x2时,y1<y2,其中正确的是( )
二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列说法:①2a+b=0,②当-1≤x≤3时,y<0;③3a+c=0;④若(x1,y1)(x2、y2)在函数图象上,当0<x1<x2时,y1<y2,其中正确的是( )| A. | ①②④ | B. | ①③ | C. | ①②③ | D. | ①③④ |
| A. |  | B. |  | C. |  | D. |  |
| A. | 9.1×10-8 | B. | 9.1×10-7 | C. | 0.91×10-8 | D. | 0.91×10-7 |
 如图,在平面直角坐标系中,直线y=-4x+4与x轴、y轴分别交于A、B两点,以AB为边在第一象限内作正方形ABCD,顶点D在双曲线y=$\frac{k}{x}$上,将该正方形沿x轴负方向平移a个单位长度后,顶点C恰好落在双曲线y=$\frac{k}{x}$上,则a的值是( )
如图,在平面直角坐标系中,直线y=-4x+4与x轴、y轴分别交于A、B两点,以AB为边在第一象限内作正方形ABCD,顶点D在双曲线y=$\frac{k}{x}$上,将该正方形沿x轴负方向平移a个单位长度后,顶点C恰好落在双曲线y=$\frac{k}{x}$上,则a的值是( )