题目内容
19.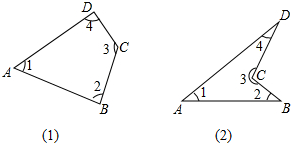 求图(1)和图(2)中的∠1+∠2+∠3+∠4的度数.
求图(1)和图(2)中的∠1+∠2+∠3+∠4的度数.
分析 图(1)中,根据四边形的内角和为360°,即可解答;
图(2)连接AC,借助于三角形内角和为180°,即可解答.
解答 解:图(1)∵四边形内角和为360°,
∴∠1+∠2+∠3+∠4=360°.
如图(2),连接AC,
在△ACD中,∠DAC+∠ACD+∠4=180°,
在△ACB中,∠BAC+∠ACB+∠2=180°,
∴∠DAC+∠ACD+∠4+∠BAC+∠ACB+∠2=360°
∵∠DAC+∠BAC=∠1,∠ACB+∠ACD=∠3,
∴∠1+∠2+∠3+∠4=360°.
点评 本题考查了多边形的内角和,解决本题的关键是借助于三角形的内角和为180°.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
10.如图,图①是一块边长为1,周长记为P1的等边三角形纸板,沿图①的底边剪去一块边长为$\frac{1}{2}$的等边三角形纸板后得到图②,然后沿同一底边依次剪去一块更小的等边三角形纸板(使其边长为前一块被剪掉正三角形纸板边长的$\frac{1}{2}$)后,得图③,④,…,记第n(n≥3)块纸板的周长为Pn,则Pn-Pn-1的值( )
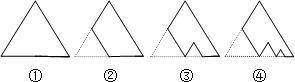

| A. | ${({\frac{1}{4}})^n}$ | B. | ${({\frac{1}{4}})^{n-1}}$ | C. | ${({\frac{1}{2}})^n}$ | D. | ${({\frac{1}{2}})^{n-1}}$ |
9.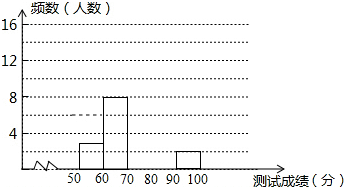 为了增强学生环保意识,我区举办了首届“环保知识大赛”,经选拔后有30名学生参加决赛,这30,名学生同事解答50个选择题,若每正确一个选择题得2分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表:
为了增强学生环保意识,我区举办了首届“环保知识大赛”,经选拔后有30名学生参加决赛,这30,名学生同事解答50个选择题,若每正确一个选择题得2分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表:
(1)求表中a的值;
(2)请把频数分布直方图补充完整;
(3)若测试成绩不低于80分为优秀,则本次测试的优秀率是多少?
(4)第4组的同学将抽出3名对第一组3名同学进行“一帮一”辅导,则第4组的小宇与小强能同时抽到的概率是多少?
 为了增强学生环保意识,我区举办了首届“环保知识大赛”,经选拔后有30名学生参加决赛,这30,名学生同事解答50个选择题,若每正确一个选择题得2分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表:
为了增强学生环保意识,我区举办了首届“环保知识大赛”,经选拔后有30名学生参加决赛,这30,名学生同事解答50个选择题,若每正确一个选择题得2分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表:| 组别 | 成绩x分 | 频数(人数) |
| 第1组 | 50≤x<60 | 3 |
| 第2组 | 60≤x<70 | 8 |
| 第3组 | 70≤x<80 | 13 |
| 第4组 | 80≤x<90 | a |
| 第5组 | 90≤x<100 | 2 |
(2)请把频数分布直方图补充完整;
(3)若测试成绩不低于80分为优秀,则本次测试的优秀率是多少?
(4)第4组的同学将抽出3名对第一组3名同学进行“一帮一”辅导,则第4组的小宇与小强能同时抽到的概率是多少?
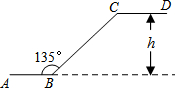 如图是石景山当代商场地下广场到地面广场的手扶电梯示意图.其中AB、CD分别表示地下广场、地面广场电梯口处的水平线.已知∠ABC=135°,BC的长约是$6\sqrt{2}$m,则乘电梯从点B到点C上升的高度h是6m.
如图是石景山当代商场地下广场到地面广场的手扶电梯示意图.其中AB、CD分别表示地下广场、地面广场电梯口处的水平线.已知∠ABC=135°,BC的长约是$6\sqrt{2}$m,则乘电梯从点B到点C上升的高度h是6m.