题目内容
4.整理一批图书,由一个人做要40小时完成,现在计划由一部分人先做4小时,再增加2人和他们一起做8小时,完成这项工作,假设这些人的工作效率相同,具体应先安排多少人工作?分析 由一个人做要40小时完成,即一个人一小时能完成全部工作的$\frac{1}{40}$,就是已知工作的效率.本题中存在的相等关系是:这部分人4小时完成的工作量+增加2人后8小时完成的工作量=全部工作量.设全部工作量是1,这部分共有x人,就可以列出方程.
解答 解:设具体应先安排x人工作,
根据题意得:$\frac{4x}{40}$+$\frac{8(x+2)}{40}$=1,
即:x+2(x+2)=10,
解得:x=2.
答:具体应先安排2人工作.
点评 本题考查了一元一次方程的应用,是一个工作效率问题,理解一个人做要40小时完成,即一个人一小时能完成全部工作的$\frac{1}{40}$,这一个关系是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19.植树节时,某班学生平均植树6棵,单独女生完成,每人应植树15棵,那么单独男生完成,每人应植树( )
| A. | 9棵 | B. | 10棵 | C. | 12棵 | D. | 14棵 |
13.等腰三角形的一边为3,另一边为6,则这个三角形的周长为( )
| A. | 15 | B. | 12或15 | C. | 9 | D. | 12 |
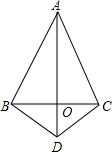 如图,在△ABC中,AB=AC,点O是BC的中点,连接AO,在AO的延长线上取一点D,连接BD,CD
如图,在△ABC中,AB=AC,点O是BC的中点,连接AO,在AO的延长线上取一点D,连接BD,CD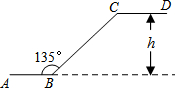 如图是石景山当代商场地下广场到地面广场的手扶电梯示意图.其中AB、CD分别表示地下广场、地面广场电梯口处的水平线.已知∠ABC=135°,BC的长约是$6\sqrt{2}$m,则乘电梯从点B到点C上升的高度h是6m.
如图是石景山当代商场地下广场到地面广场的手扶电梯示意图.其中AB、CD分别表示地下广场、地面广场电梯口处的水平线.已知∠ABC=135°,BC的长约是$6\sqrt{2}$m,则乘电梯从点B到点C上升的高度h是6m.