题目内容
19.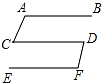 如图,AB∥CD∥EF,AC∥DF,若∠BAC=150°,则∠CDF=( )
如图,AB∥CD∥EF,AC∥DF,若∠BAC=150°,则∠CDF=( )| A. | 30° | B. | 60° | C. | 150° | D. | 150° |
分析 根据两直线平行,同旁内角互补由AB∥CD得到∠BAC+∠ACD=180°,可计算出∠ACD=30°,然后由AC∥DF,根据平行线的性质得到∠ACD=∠CDF=00°.
解答 解:∵AB∥CD,
∴∠BAC+∠ACD=180°,
∵∠BAC=150°,
∴∠ACD=180°-130°=30°,
∵AC∥DF,
∴∠ACD=∠CDF,
∴∠CDF=30°.
故选A.
点评 本题考查了平行线的性质:两直线平行,内错角相等;两直线平行,同旁内角互补.

练习册系列答案
相关题目
9.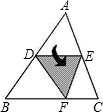 如图,D、E为△ABC两边AB、AC上的两点,将△ABC沿线段DE折叠,使得DE∥BC,且点A落在点F处,若∠B=55°,则∠BDF为( )
如图,D、E为△ABC两边AB、AC上的两点,将△ABC沿线段DE折叠,使得DE∥BC,且点A落在点F处,若∠B=55°,则∠BDF为( )
 如图,D、E为△ABC两边AB、AC上的两点,将△ABC沿线段DE折叠,使得DE∥BC,且点A落在点F处,若∠B=55°,则∠BDF为( )
如图,D、E为△ABC两边AB、AC上的两点,将△ABC沿线段DE折叠,使得DE∥BC,且点A落在点F处,若∠B=55°,则∠BDF为( )| A. | 55° | B. | 60° | C. | 70° | D. | 不能确定 |
8.9的算术平方根是( )
| A. | 3 | B. | -3 | C. | 9 | D. | ±3 |

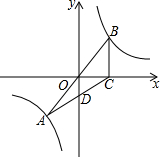 如图,A、B是反比例函数y=$\frac{k}{x}$图象上关于原点O对称的两点,BC⊥x轴,垂足为C,连线AC过点D(0,-1.5).若△ABC的面积为7,则点B的坐标为($\frac{7}{3}$,3).
如图,A、B是反比例函数y=$\frac{k}{x}$图象上关于原点O对称的两点,BC⊥x轴,垂足为C,连线AC过点D(0,-1.5).若△ABC的面积为7,则点B的坐标为($\frac{7}{3}$,3).