题目内容
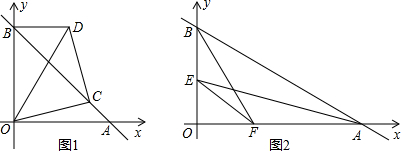
如图1,已知A(a,0),B(0,b).
(1)当a、b满足a2-8a+b2-8b+32=0时,求∠BAO的度数;
(2)如图1,在(1)的条件下,点C为线段AB上一点(BC>CA),以点C为直角顶点,OC为腰作等腰Rt△OCD,连接BD,求证:∠BDO=∠BCO;
(3)如图2,△ABO的两条角平分线AE、BF交于点Q,若△ABQ的面积为24,求四边形AFEB的面积.
(1)当a、b满足a2-8a+b2-8b+32=0时,求∠BAO的度数;
(2)如图1,在(1)的条件下,点C为线段AB上一点(BC>CA),以点C为直角顶点,OC为腰作等腰Rt△OCD,连接BD,求证:∠BDO=∠BCO;
(3)如图2,△ABO的两条角平分线AE、BF交于点Q,若△ABQ的面积为24,求四边形AFEB的面积.

考点:全等三角形的判定与性质,坐标与图形性质
专题:
分析:(1)根据平方值的非负性质即可求得a、b的值,即可解题;
(2)过C作EF∥OB交OA于F,交BD延长线于点E,易证∠COF=∠DCE,即可证明△COF≌△DCE,可得CE=OF,即可求得EF=OB,即可证明四边形OFEB为矩形,即可求得∠BDO=∠DOF,易证∠DOF=∠BCO,即可解题;
(3)过E作EG⊥BF交AB于G,过F作FH⊥AE分别交AE、AB于M、H,过H作HN⊥QG于N点,易证BE=BG,即可证明△BQE≌△BGQ,同理可得△AQH≌△AQF,易证S△EQF=S△GQH,可得S△AQB=S△BQE+S△AQF+S△EQF,即可求得四边形AFEB的面积,即可解题.
(2)过C作EF∥OB交OA于F,交BD延长线于点E,易证∠COF=∠DCE,即可证明△COF≌△DCE,可得CE=OF,即可求得EF=OB,即可证明四边形OFEB为矩形,即可求得∠BDO=∠DOF,易证∠DOF=∠BCO,即可解题;
(3)过E作EG⊥BF交AB于G,过F作FH⊥AE分别交AE、AB于M、H,过H作HN⊥QG于N点,易证BE=BG,即可证明△BQE≌△BGQ,同理可得△AQH≌△AQF,易证S△EQF=S△GQH,可得S△AQB=S△BQE+S△AQF+S△EQF,即可求得四边形AFEB的面积,即可解题.
解答:解:(1)∵a2-8a+b2-8b+32=0,
∴a2-8a+16+b2-8b+16=0,即(a-4)2+(b-4)2=0,
∴a=b=4,
∴∠BAO=45°;
(2)过C作EF∥OB交OA于F,交BD延长线于点E,
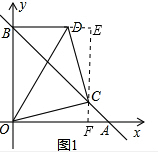
则∠OFC=∠CED=90°,
∵∠OCF+∠COF=90°,∠OCF+∠DCE=90°,
∴∠COF=∠DCE,
在△COF和△DCE中,
,
∴△COF≌△DCE,(AAS)
∴CE=OF,
∵∠BAO=45°,∠CFA=90°,
∴AF=CF,
∴EF=CE+CF=OF+AF=OA=OB,
∴四边形OFEB为矩形,
∴BD∥OA,
∴∠BDO=∠DOF,
∵∠DOF=∠COD+∠COF,∠BCO=∠BAO+∠COF,∠COD=∠BAO=45°,
∴∠DOF=∠BCO,
∴∠BDO=∠BCO.
(3)过E作EG⊥BF交AB于G,过F作FH⊥AE分别交AE、AB于M、H,过H作HN⊥QG于N点,
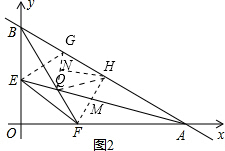
∵BF平分∠ABO,EG⊥BQ,
∴BQ是EG垂直平分线,
∴BE=BG,
在△BQE和△BGQ中,
,
∴△BQE≌△BGQ,(SAS)
同理△AQH≌△AQF,
∵∠AOB=90°,
∴∠OAB+∠OBA=90°.
∵BF平分∠OBA,AE平分∠OAB,
∴∠ABQ+∠BAQ=45°,
∴∠GQH=∠HQM=45°,
∴四边形QMHN是矩形,
∵FH⊥AE,
∴QM=HM,
∴四边形QMHN是正方形,
∴NH=HM,
∵HM=FM,
∴MF=HN,
∴S△EQF=S△GQH,
∴S△AQB=S△BQE+S△AQF+S△EQF=24,
∴S四边形AFEB=24×2=48.
∴a2-8a+16+b2-8b+16=0,即(a-4)2+(b-4)2=0,
∴a=b=4,
∴∠BAO=45°;
(2)过C作EF∥OB交OA于F,交BD延长线于点E,

则∠OFC=∠CED=90°,
∵∠OCF+∠COF=90°,∠OCF+∠DCE=90°,
∴∠COF=∠DCE,
在△COF和△DCE中,
|
∴△COF≌△DCE,(AAS)
∴CE=OF,
∵∠BAO=45°,∠CFA=90°,
∴AF=CF,
∴EF=CE+CF=OF+AF=OA=OB,
∴四边形OFEB为矩形,
∴BD∥OA,
∴∠BDO=∠DOF,
∵∠DOF=∠COD+∠COF,∠BCO=∠BAO+∠COF,∠COD=∠BAO=45°,
∴∠DOF=∠BCO,
∴∠BDO=∠BCO.
(3)过E作EG⊥BF交AB于G,过F作FH⊥AE分别交AE、AB于M、H,过H作HN⊥QG于N点,

∵BF平分∠ABO,EG⊥BQ,
∴BQ是EG垂直平分线,
∴BE=BG,
在△BQE和△BGQ中,
|
∴△BQE≌△BGQ,(SAS)
同理△AQH≌△AQF,
∵∠AOB=90°,
∴∠OAB+∠OBA=90°.
∵BF平分∠OBA,AE平分∠OAB,
∴∠ABQ+∠BAQ=45°,
∴∠GQH=∠HQM=45°,
∴四边形QMHN是矩形,
∵FH⊥AE,
∴QM=HM,
∴四边形QMHN是正方形,
∴NH=HM,
∵HM=FM,
∴MF=HN,
∴S△EQF=S△GQH,
∴S△AQB=S△BQE+S△AQF+S△EQF=24,
∴S四边形AFEB=24×2=48.
点评:本题考查了全等三角形的判定,考查了全等三角形对应边相等的性质,本题中求证△COF≌△DCE、△BQE≌△BGQ和△AQH≌△AQF是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
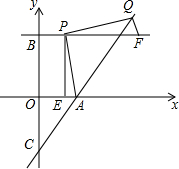 在平面直角坐标系中,A(2,0)、B(0,3),过点B作直线∥x轴,点P(a,3)是直线上的动点,以AP为边在AP右侧作等腰Rt△APQ,∠APQ=Rt∠,直线AQ交y轴于点C
在平面直角坐标系中,A(2,0)、B(0,3),过点B作直线∥x轴,点P(a,3)是直线上的动点,以AP为边在AP右侧作等腰Rt△APQ,∠APQ=Rt∠,直线AQ交y轴于点C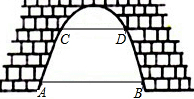 如图,有一座抛物线形拱桥,已知桥下在正常水位AB时,水面宽8m,水位上升3m,就达到警戒水位CD,这时水面宽4m,若洪水到来时,水位以每小时0.2m的速度上升,求水过警戒水位后几小时淹到桥拱顶.
如图,有一座抛物线形拱桥,已知桥下在正常水位AB时,水面宽8m,水位上升3m,就达到警戒水位CD,这时水面宽4m,若洪水到来时,水位以每小时0.2m的速度上升,求水过警戒水位后几小时淹到桥拱顶.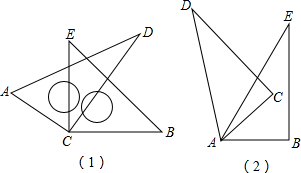 如图(1),将两块直角三角尺的直角顶点C叠放在一起,
如图(1),将两块直角三角尺的直角顶点C叠放在一起,