题目内容
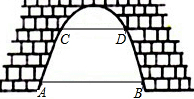 如图,有一座抛物线形拱桥,已知桥下在正常水位AB时,水面宽8m,水位上升3m,就达到警戒水位CD,这时水面宽4m,若洪水到来时,水位以每小时0.2m的速度上升,求水过警戒水位后几小时淹到桥拱顶.
如图,有一座抛物线形拱桥,已知桥下在正常水位AB时,水面宽8m,水位上升3m,就达到警戒水位CD,这时水面宽4m,若洪水到来时,水位以每小时0.2m的速度上升,求水过警戒水位后几小时淹到桥拱顶.考点:二次函数的应用
专题:
分析:以AB为x轴,中点为坐标原点建立平面直角坐标系,已知B、D可得y的解析式,从而求出OM的值.又因为MN=OM-ON,故可求t的值.
解答:解:根据题意建立坐标系如下:

设抛物线解析式为:y=ax2+h,
又∵B(4,0),D(2,3)
∴
,
解得:
,
∴y=-
x2+4,
∴M(0,4)即OM=6m
∴MN=OM-ON=31,
则t=
=5(小时).
答:水过警戒线后5小时淹到拱桥顶.

设抛物线解析式为:y=ax2+h,
又∵B(4,0),D(2,3)
∴
|
解得:
|
∴y=-
| 1 |
| 4 |
∴M(0,4)即OM=6m
∴MN=OM-ON=31,
则t=
| MN |
| 0.2 |
答:水过警戒线后5小时淹到拱桥顶.
点评:本题考查二次函数的实际应用.此题为数学建模题,借助二次函数解决实际问题.

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
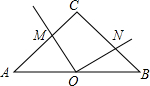 等腰直角△ABC中,∠C=90°,O是AB的中点,∠MON=90°,AC=12.求四边形OMCN的面积.
等腰直角△ABC中,∠C=90°,O是AB的中点,∠MON=90°,AC=12.求四边形OMCN的面积.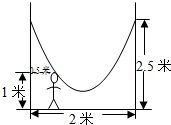 如图,小明的父亲在相距2米的两棵树间拴了一根绳子,给他做了一个简易的秋千,拴绳子的地方距地面高都是2.5米,绳子自然下垂呈抛物线状,身高1米的小明距较近的那棵树0.5米时,头部刚好接触到绳子,则绳子的最低点距地面的距离为( )米.
如图,小明的父亲在相距2米的两棵树间拴了一根绳子,给他做了一个简易的秋千,拴绳子的地方距地面高都是2.5米,绳子自然下垂呈抛物线状,身高1米的小明距较近的那棵树0.5米时,头部刚好接触到绳子,则绳子的最低点距地面的距离为( )米.