题目内容
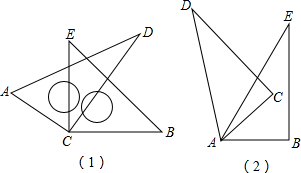 如图(1),将两块直角三角尺的直角顶点C叠放在一起,
如图(1),将两块直角三角尺的直角顶点C叠放在一起,(1)若∠DCE=25°,∠ACB=
(2)猜想∠ACB与∠DCE的大小有何特殊关系,并说明理由;
(3)如图(2),若是两个同样的直角三角尺60°锐角的顶点A重合在一起,则∠DAB与∠CAE的大小又有何关系,请说明理由.
考点:余角和补角,角的计算
专题:
分析:(1)本题已知两块直角三角尺实际就是已知三角板的各个角的度数,根据角的和差就可以求出∠ACB,∠DCE的度数;
(2)根据前个小问题的结论猜想∠ACB与∠DCE的大小关系,结合前问的解决思路得出证明.
(3)根据(1)(2)解决思路确定∠DAB与∠CAE的大小并证明.
(2)根据前个小问题的结论猜想∠ACB与∠DCE的大小关系,结合前问的解决思路得出证明.
(3)根据(1)(2)解决思路确定∠DAB与∠CAE的大小并证明.
解答:解:(1)∵∠ECB=90°,∠DCE=25°
∴∠DCB=90°-25°=65°
∵∠ACD=90°
∴∠ACB=∠ACD+∠DCB=155°.
∵∠ACB=150°,∠ACD=90°
∴∠DCB=150°-90°=60°
∵∠ECB=90°
∴∠DCE=90°-60°=30°.
故答案为:155°,30°;
(2)猜想得:∠ACB+∠DCE=180°(或∠ACB与∠DCE互补)
理由:∵∠ECB=90°,∠ACD=90°
∴∠ACB=∠ACD+∠DCB=90°+∠DCB
∠DCE=∠ECB-∠DCB=90°-∠DCB
∴∠ACB+∠DCE=180°;
(3)∠DAB+∠CAE=120°
理由如下:
∵∠DAB=∠DAE+∠CAE+∠CAB
故∠DAB+∠CAE=∠DAE+∠CAE+∠CAB+∠CAE=∠DAC+∠BAE=120°.
∴∠DCB=90°-25°=65°
∵∠ACD=90°
∴∠ACB=∠ACD+∠DCB=155°.
∵∠ACB=150°,∠ACD=90°
∴∠DCB=150°-90°=60°
∵∠ECB=90°
∴∠DCE=90°-60°=30°.
故答案为:155°,30°;
(2)猜想得:∠ACB+∠DCE=180°(或∠ACB与∠DCE互补)
理由:∵∠ECB=90°,∠ACD=90°
∴∠ACB=∠ACD+∠DCB=90°+∠DCB
∠DCE=∠ECB-∠DCB=90°-∠DCB
∴∠ACB+∠DCE=180°;
(3)∠DAB+∠CAE=120°
理由如下:
∵∠DAB=∠DAE+∠CAE+∠CAB
故∠DAB+∠CAE=∠DAE+∠CAE+∠CAB+∠CAE=∠DAC+∠BAE=120°.
点评:此题考查了余角和补角、角的计算及直角三角形的性质,解题关键是:记忆三角板各角的度数,把所求的角转化为已知角的和与差.

练习册系列答案
相关题目
下列计算正确的是( )
| A、3a-a=2 |
| B、a2•a3=a6 |
| C、a2+2a2=3a2 |
| D、(a+b)2=a2+b2 |
 已知在△ABC中,∠ABC=∠ACB,∠1=∠2,求证:AD平分∠BAC.
已知在△ABC中,∠ABC=∠ACB,∠1=∠2,求证:AD平分∠BAC. 如图,△ABC中,点D、E分别为AB、AC的中点,连接DE,线段BE、CD相交于点O,则
如图,△ABC中,点D、E分别为AB、AC的中点,连接DE,线段BE、CD相交于点O,则 如图,已知∠AOB是直角,COD是一条直线,∠AOC=25°,则∠BOD=
如图,已知∠AOB是直角,COD是一条直线,∠AOC=25°,则∠BOD= 如图,已知△ABC.利用直尺和圆规,根据要求作图,并解决后面的问题.
如图,已知△ABC.利用直尺和圆规,根据要求作图,并解决后面的问题.