题目内容
如图，将一正方形纸片沿图（1）、（2）的虚线对折，得到图（3），然后沿图（3）中虚线的剪去一个角，展开得平面图形（4），则图（3）的虚线是（ ）
A．
B．
C．
D．
D
【解析】
试题分析：对于此类问题，学生只要亲自动手操作，答案就会很直观地呈现．
【解析】
由于得到的图形的中间是正方形，那么它的四分之一为等腰直角三角形．
故选D．
天天向上一本好卷系列答案
小学生10分钟应用题系列答案一个多边形切去一个角后，形成的另一个多边形的内角和为1080°，那么原多边形的边数为（ ）
A．7 B．7或8 C．8或9 D．7或8或9
D．
【解析】
试题分析：设内角和为1080°的多边形的边数是n，则（n﹣2）•180°=1080°，解得：n=8．
则原多边形的边数为7或8或9．故选D． 从2，3，4，5，6中任取两个数就组成一组数，其中两数之和小于10的数组共有 组．
8
【解析】
试题分析：将所有情况列举出来，然后判断即可．
【解析】
从2，3，4，5，6中任取两个数就组成一组数，可能为2+3=5，2+4=6，2+5=7，2+6=8，3+4=7，3+5=8，3+6=9，4+5=9，4+6=10，5+6=11，
其中小于10的有8组，
故答案为：8． 如图，△ABE和△ADC是△ABC分别沿AB、AC边翻折得到的，若∠1: ∠2:∠3 = 28 :5 : 3， 则∠4的度数为__________
80°
【解析】根据翻折求出各个角的度数，再根据三角形的一个外角等于和它不相邻的两个内角的和求出∠4的度数.
【解析】
∵∠1: ∠2:∠3 = 28 :5 : 3，
∠1+∠2+∠3 = 180°，
∴∠1=140°，∠2=25°，∠3=15°，
由翻折得∠EBA =∠2 =25°，∠DCA =∠3 =15°，
∴∠EBC=∠EBA +∠2 =50°，∠DC... 如图，△ABC和△A′B′C′关于直线l对称，下列结论中：
①△ABC≌△A′B′C′；
②∠BAC′=∠B′AC；
③l垂直平分CC′；
④直线BC和B′C′的交点不一定在l上，
正确的有（ ）
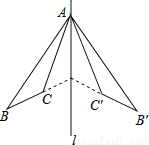
A. 4个 B. 3个 C. 2个 D. 1个
B
【解析】【解析】
∵△ABC和△A′B′C′关于直线l对称，
∴①△ABC≌△A′B′C′，正确；
②∠BAC=∠B′AC′，
∴∠BAC+∠CAC′=∠B′AC′+∠CAC′，
即∠BAC′=∠B′AC正确；
③l垂直平分CC′，正确；
④应为：直线BC和B′C′的交点一定在l上，故本小题错误．
综上所述，结论正确的是①②③共3个．
故... 对于下列命题：（1）关于某一直线成轴对称的两个三角形全等；（2）等腰三角形的对称轴是顶角的平分线；（3）一条线段的两个端点一定是关于经过该线段中点的直线的对称点；（4）如果两个三角形全等，那么它们关于某直线成轴对称。其中真命题的个数为
A、0 B、1 C、2 D、3
C
【解析】
试题分析：根据平面图形的基本概念依次分析各小题即可作出判断.
（1）关于某一直线成轴对称的两个三角形全等，（3）一条线段的两个端点一定是关于经过该线段中点的直线的对称点，均为真命题；
（2）等腰三角形的对称轴是顶角的平分线所在的直线，（4）如果两个三角形全等，它们可能是平移或旋转构成的，均为假命题；
故选C. 如图,∠AOB内一点P,分别画出P关于OA、OB的对称点P1、P2连P1P2交OA于M,交OB于N,若P1P2=5cm,则△PMN的周长为_______.
5cm
【解析】∵P、P1,P、P2关于OA、OB对称，
∴PM=P1M,PN=P2N，
∴△PMN的周长=P1P2，
∴△PMN的周长是5 cm. 下列说法错误的是( )
A. 等边三角形是轴对称图形
B. 轴对称图形的对应边相等,对应角相等
C. 成轴对称的两条线段必在对称轴一侧
D. 成轴对称的两个图形对应点的连线被对称轴垂直平分
C
【解析】A. 由等边三角形的性质知,等边三角形是轴对称图形,正确;
B. 由轴对称的性质知,轴对称图形的对应边相等,对应角相等,正确;
C. 成轴对称的两条线段必在对称轴两侧,故错误;
D. 由轴对称的性质知,成轴对称的两个图形对应点的连线被对称轴垂直平分,正确;
故选C. 下列事件中,是必然事件的是( )
A. 两条线段可以组成一个三角形
B. 400人中有两个人的生日在同一天
C. 早上的太阳从西方升起
D. 打开电视机,它正在播放动画片
B
【解析】试题解析：A. 两条线段可以组成一个三角形是不可能事件，故错误；
B.400人中有两个人的生日在同一天是必然事件，故正确；
C. 早上的太阳从西方升起是不可能事件，故错误；
D. 打开电视机，它正在播放动画片是随机事件，故错误；
故选B.