题目内容
19．
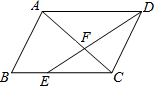?ABCD中，E在BC上，且CE=2BE，AC与DE相交于F，若S△FEC=8．则S△DFC=12，S△AFD=18．
分析 由四边形ABCD是平行四边形，易证得△DAF∽△ECF，又由CE=2BE，可得AD：CE=3：2，由等高三角形的面积比等于对应底的比，得出S△DFC：S△FEC=DF：EF=3：2，求出S△DFC=8×3÷2=12；根据相似三角形的面积比等于相似比的平方，得出S△AFD：S△FEC=（AD：CE）2=9：4，求得S△AFD=8×9÷4=18．
解答 解：∵四边形ABCD是平行四边形，
∴AD∥BC，AD=BC，
∴△DAF∽△ECF，
∴DF：EF=AD：CE，
∵CE=2BE，
∴CE：BC=2：3，
∴BC：CE=3：2，即AD：CE=3：2，
∴S△DFC：S△FEC=DF：EF=3：2，
∴S△DFC=8×3÷2=12；
S△AFD：S△FEC=（AD：CE）2=9：4，
∴S△AFD=8×9÷4=18．
故答案为12，18．
点评 本题考查了相似三角形的判定与性质，利用了相似三角形的面积比等于相似比的平方，利用等高三角形的面积比等于底边之比．
练习册系列答案
相关题目
如图，线段AB是⊙O的直径，弦CD⊥AB，∠DAB=70°，则∠COB等于140度．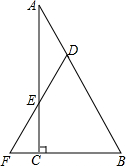
如图，在Rt△ABC中，在斜边AB和直角边AC上分别取一点D，E，使DE=DA，延长DE交BC的延长线于点F．△DFB是等腰三角形吗？请说明你的理由．
已知，如图△ABC中，AB=AC，∠A=50°，BD=CE，BF=CD，求∠FDE的度数．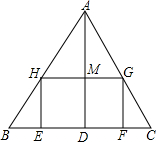
如图，△ABC，是一张锐角三角形的硬纸片，AD是边BC上的高，BC=40cm，AD=30cm，从这张硬纸片上剪下一个矩形EFGH，使它的一边EF在BC上，顶点G、H分别在AC，AB上，AD与HG的交点为M．
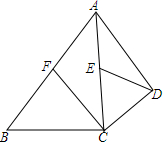如图，在四边形ABCD中，$\frac{BC}{CD}$=$\frac{3}{2}$，AC平分∠BAD，∠ACB=∠ADC=90°，CF和DE是△ABC、△ACD的中线，求$\frac{CE}{DE}$的值．
如图，已知$\frac{AD}{AB}$=$\frac{DE}{BC}$=$\frac{AE}{AC}$，求证：∠ABD=∠ACE．