题目内容
5.已知$\frac{1}{1\sqrt{2}+2\sqrt{1}}$+$\frac{1}{2\sqrt{3}+3\sqrt{2}}$+$\frac{1}{3\sqrt{4}+4\sqrt{3}}$+…+$\frac{1}{n\sqrt{n+1}+(n+1)\sqrt{n}}$=$\frac{49}{50}$,则n=2499.分析 首先把分母有理化,进一步计算得出结果建立关于n的方程,求得方程的解即可.
解答 解:$\frac{1}{1\sqrt{2}+2\sqrt{1}}$+$\frac{1}{2\sqrt{3}+3\sqrt{2}}$+$\frac{1}{3\sqrt{4}+4\sqrt{3}}$+…+$\frac{1}{n\sqrt{n+1}+(n+1)\sqrt{n}}$=$\frac{49}{50}$,
$\frac{2-\sqrt{2}}{2}$+$\frac{3\sqrt{2}-2\sqrt{3}}{6}$+$\frac{4\sqrt{3}-3\sqrt{4}}{12}$+…+$\frac{(n+1)\sqrt{n}-n\sqrt{n+1}}{n(n+1)}$=$\frac{49}{50}$
1-$\frac{\sqrt{n+1}}{n+1}$=$\frac{49}{50}$
$\frac{1}{\sqrt{n+1}}$=$\frac{1}{50}$
$\sqrt{n+1}$=50
n+1=2500
n=2499.
经检验n=2499是原方程的解.
故答案为:2499.
点评 此题考查分母有理化,主要利用平方差公式解决问题.

练习册系列答案
相关题目
13. 如图,直角△ABC沿直角边BC所在的直线向右平移得到△DEF,则下列结论中错误的是( )
如图,直角△ABC沿直角边BC所在的直线向右平移得到△DEF,则下列结论中错误的是( )
 如图,直角△ABC沿直角边BC所在的直线向右平移得到△DEF,则下列结论中错误的是( )
如图,直角△ABC沿直角边BC所在的直线向右平移得到△DEF,则下列结论中错误的是( )| A. | ∠ACB=∠DFE | B. | BE=CF | C. | AB∥DE | D. | AG=CG |
15.以下列各组长度的线段为边,能构成三角形的是( )
| A. | 7cm,5cm,12cm | B. | 6cm,8cm,15cm | C. | 4cm,6cm,5cm | D. | 8cm,4cm,3cm |
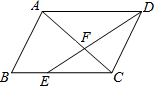 ?ABCD中,E在BC上,且CE=2BE,AC与DE相交于F,若S△FEC=8.则S△DFC=12,S△AFD=18.
?ABCD中,E在BC上,且CE=2BE,AC与DE相交于F,若S△FEC=8.则S△DFC=12,S△AFD=18.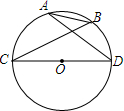 如图,在⊙O中,CD为直径,CD=3,AB=1.求cosα的值.
如图,在⊙O中,CD为直径,CD=3,AB=1.求cosα的值. 如图,⊙O的弦ED,CB的延长线交于点A,若BD⊥AE,AB=4,BC=2,AD=3,则DE=5,CD=3$\sqrt{2}$.
如图,⊙O的弦ED,CB的延长线交于点A,若BD⊥AE,AB=4,BC=2,AD=3,则DE=5,CD=3$\sqrt{2}$. 如图,在菱形ABCD中,AB=2,∠C=60°,E是边AD中点,F是边AB上一点(不与点A重合)延长FE交CD的延长线于点G,连接FD,AG.
如图,在菱形ABCD中,AB=2,∠C=60°,E是边AD中点,F是边AB上一点(不与点A重合)延长FE交CD的延长线于点G,连接FD,AG. 如图,△ABC中,D、E分别是AB、AC的中点.求证:DE=$\frac{1}{2}$BC,DE∥BC.
如图,△ABC中,D、E分别是AB、AC的中点.求证:DE=$\frac{1}{2}$BC,DE∥BC.