题目内容
8. 如图,已知$\frac{AD}{AB}$=$\frac{DE}{BC}$=$\frac{AE}{AC}$,求证:∠ABD=∠ACE.
如图,已知$\frac{AD}{AB}$=$\frac{DE}{BC}$=$\frac{AE}{AC}$,求证:∠ABD=∠ACE.
分析 根据$\frac{AD}{AB}$=$\frac{DE}{BC}$=$\frac{AE}{AC}$,得到△ADE∽△ABC,根据相似三角形的性质得到∠DAE=∠BAC,根据角的和差得到∠DAB=∠EAC,推出△ADB∽△AEC,即可得到结论.
解答 解:∵$\frac{AD}{AB}$=$\frac{DE}{BC}$=$\frac{AE}{AC}$,
∴△ADE∽△ABC,
∴∠DAE=∠BAC,
∴∠DAB=∠EAC,
∵$\frac{AD}{AB}=\frac{AE}{AC}$,
∴△ADB∽△AEC,
∴∠ABD=∠ACE.
点评 本题考查了相似三角形的判定和性质,熟练掌握相似三角形的判定和性质是解题的关键.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
13. 如图,直角△ABC沿直角边BC所在的直线向右平移得到△DEF,则下列结论中错误的是( )
如图,直角△ABC沿直角边BC所在的直线向右平移得到△DEF,则下列结论中错误的是( )
 如图,直角△ABC沿直角边BC所在的直线向右平移得到△DEF,则下列结论中错误的是( )
如图,直角△ABC沿直角边BC所在的直线向右平移得到△DEF,则下列结论中错误的是( )| A. | ∠ACB=∠DFE | B. | BE=CF | C. | AB∥DE | D. | AG=CG |
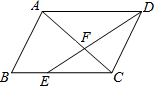 ?ABCD中,E在BC上,且CE=2BE,AC与DE相交于F,若S△FEC=8.则S△DFC=12,S△AFD=18.
?ABCD中,E在BC上,且CE=2BE,AC与DE相交于F,若S△FEC=8.则S△DFC=12,S△AFD=18. 如图,抛物线y=-x2+4ax-3经过点M(2,1),交x轴于A、B,交y轴负半轴于C,平移CM交x轴于D,交对称轴右边的抛物线于P,使DP=CM,求点P的坐标.
如图,抛物线y=-x2+4ax-3经过点M(2,1),交x轴于A、B,交y轴负半轴于C,平移CM交x轴于D,交对称轴右边的抛物线于P,使DP=CM,求点P的坐标. 如图,在Rt△ACB内作边长依次为m、n、p(m>n>p)的三个正方形,设BC=a,AC=b.
如图,在Rt△ACB内作边长依次为m、n、p(m>n>p)的三个正方形,设BC=a,AC=b.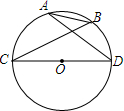 如图,在⊙O中,CD为直径,CD=3,AB=1.求cosα的值.
如图,在⊙O中,CD为直径,CD=3,AB=1.求cosα的值.