题目内容
7.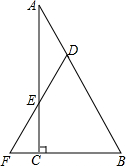 如图,在Rt△ABC中,在斜边AB和直角边AC上分别取一点D,E,使DE=DA,延长DE交BC的延长线于点F.△DFB是等腰三角形吗?请说明你的理由.
如图,在Rt△ABC中,在斜边AB和直角边AC上分别取一点D,E,使DE=DA,延长DE交BC的延长线于点F.△DFB是等腰三角形吗?请说明你的理由.
分析 根据等腰三角形的性质,得出∠A=∠AED,根据对顶角相等得出∠AED=∠CEF,由直角三角形的两个锐角互余,得出∠B=∠F,则DB=DF,即可证明△DFB是等腰三角形.
解答 证明:△DFB是等腰三角形.
理由是:∵DE=DA,
∴∠A=∠AED,
∵∠AED=∠CEF,
∵∠A=∠CEF,
∵∠ACB=∠ECF=90°,
∴∠A+∠B=∠CEF+∠F,
∴∠B=∠F,
∴DB=DF,
∴△DFB是等腰三角形.
点评 本题考查了等腰三角形的判定,以及直角三角形的两个锐角互余的性质,掌握等角对等边是解题的关键.

练习册系列答案
相关题目
17.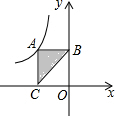 如图,点A是反比例函数y=-$\frac{6}{x}$(x<0)的图象上一点,AB⊥y轴于B,点C是x轴上任意一点,则S△ABC等于( )
如图,点A是反比例函数y=-$\frac{6}{x}$(x<0)的图象上一点,AB⊥y轴于B,点C是x轴上任意一点,则S△ABC等于( )
 如图,点A是反比例函数y=-$\frac{6}{x}$(x<0)的图象上一点,AB⊥y轴于B,点C是x轴上任意一点,则S△ABC等于( )
如图,点A是反比例函数y=-$\frac{6}{x}$(x<0)的图象上一点,AB⊥y轴于B,点C是x轴上任意一点,则S△ABC等于( )| A. | 12 | B. | 6 | C. | 3 | D. | $\frac{3}{2}$ |
13. 如图,直角△ABC沿直角边BC所在的直线向右平移得到△DEF,则下列结论中错误的是( )
如图,直角△ABC沿直角边BC所在的直线向右平移得到△DEF,则下列结论中错误的是( )
 如图,直角△ABC沿直角边BC所在的直线向右平移得到△DEF,则下列结论中错误的是( )
如图,直角△ABC沿直角边BC所在的直线向右平移得到△DEF,则下列结论中错误的是( )| A. | ∠ACB=∠DFE | B. | BE=CF | C. | AB∥DE | D. | AG=CG |
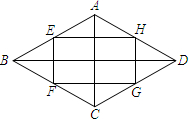 如图,顺次连接菱形ABCD的各边中点E,F,G,H,若AC=6,BD=12,则四边形EFGH的面积为18.
如图,顺次连接菱形ABCD的各边中点E,F,G,H,若AC=6,BD=12,则四边形EFGH的面积为18.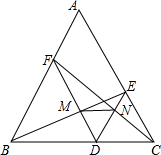 如图,在正△ABC中,DE∥AB,DF∥AC,求证:△MDN是等边三角形.
如图,在正△ABC中,DE∥AB,DF∥AC,求证:△MDN是等边三角形.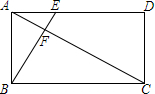 如图,在矩形ABCD中,AB=4cm,AD=8cm,点E在边AD上,AE:ED=1:3,AC、BE交于点F.
如图,在矩形ABCD中,AB=4cm,AD=8cm,点E在边AD上,AE:ED=1:3,AC、BE交于点F.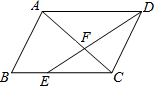 ?ABCD中,E在BC上,且CE=2BE,AC与DE相交于F,若S△FEC=8.则S△DFC=12,S△AFD=18.
?ABCD中,E在BC上,且CE=2BE,AC与DE相交于F,若S△FEC=8.则S△DFC=12,S△AFD=18.