题目内容
16.化简:$\frac{a+1}{{a}^{2}+1}$+$\frac{{(a+1)}^{3}}{{a}^{4}-1}$-$\frac{a-3}{a+1}$.分析 根据分式的运算法则即可求出答案.
解答 解:原式=$\frac{a+1}{{a}^{2}+1}$+$\frac{(a+1)^{3}}{({a}^{2}-1)({a}^{2}+1)}$-$\frac{a-3}{a+1}$,
=$\frac{a+1}{{a}^{2}+1}$+$\frac{(a+1)^{2}}{(a-1)({a}^{2}+1)}$-$\frac{a-3}{a+1}$,
=$\frac{{a}^{2}-1}{(a-1)({a}^{2}+1)}$+$\frac{(a+1)^{2}}{(a-1)({a}^{2}+1)}$-$\frac{a-3}{a+1}$,
=$\frac{2{a}^{2}+2a}{(a-1)({a}^{2}+1)}$-$\frac{a-3}{a+1}$,
=$\frac{2a(a+1)^{2}}{(a-1)(a+1)({a}^{2}+1)}$-$\frac{(a-3)(a-1)({a}^{2}+1)}{(a-1)(a+1)({a}^{2}+1)}$,
=$\frac{-{a}^{4}+6{a}^{3}+6a-3}{{a}^{4}-1}$.
点评 本题考查了分式的加减法,要牢记异分母分式加减法法则:把分母不相同的几个分式化成分母相同的分式,叫做通分,经过通分,异分母分式的加减就转化为同分母分式的加减.

练习册系列答案
相关题目
6.海中有A、B、C三个小岛,A岛在B岛正西方距离400海里处(如图所示),C岛在B岛的北偏东37°方向500海里处.

(1)用1厘米代表200海里,请根据题意在图中画出C岛的位置;量出图中AC的长度为4厘米.(四舍五入到整厘米数);那么A、C两地的实际距离约为800海里.
(2)甲、乙两货轮同时从A岛出发,甲沿A-C-B方向,乙沿A-B-C方向,10小时相遇,此时甲货轮比乙货轮多行驶了100海里,求甲乙两货轮的速度.
(3)若B岛需要大米和玉米共30吨,C岛需要大米和玉米共50吨,现从A岛运输20吨大米与60吨玉米到B岛和C岛,运输费用共为10600元(每吨的运输费用如下表所示)那么运到B岛的大米与玉米各是多少吨?:

(1)用1厘米代表200海里,请根据题意在图中画出C岛的位置;量出图中AC的长度为4厘米.(四舍五入到整厘米数);那么A、C两地的实际距离约为800海里.
(2)甲、乙两货轮同时从A岛出发,甲沿A-C-B方向,乙沿A-B-C方向,10小时相遇,此时甲货轮比乙货轮多行驶了100海里,求甲乙两货轮的速度.
(3)若B岛需要大米和玉米共30吨,C岛需要大米和玉米共50吨,现从A岛运输20吨大米与60吨玉米到B岛和C岛,运输费用共为10600元(每吨的运输费用如下表所示)那么运到B岛的大米与玉米各是多少吨?:
| 到B岛的运费(元/吨) | 到C岛的运费(元/吨) | |
| 大米 | 100 | 200 |
| 玉米 | 80 | 150 |
8.若a=3,a-b=2,则a2-ab的值为( )
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
5.如果把分式$\frac{{3n}^{2}}{m-n}$中的m和n都扩大3倍,那么分式的值( )
| A. | 不变 | B. | 扩大3倍 | C. | 缩小3倍 | D. | 扩大9倍 |
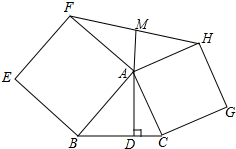 如图,在△ABC的两边AB,AC上向△ABC外作正方形ABEF,ACGH,过点A作BC的垂线分别交BC于点D,交FH于点M,求证:FM=MH.
如图,在△ABC的两边AB,AC上向△ABC外作正方形ABEF,ACGH,过点A作BC的垂线分别交BC于点D,交FH于点M,求证:FM=MH.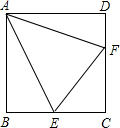 如图,点E,F分别为正方形ABCD的边BC、CD上一点,且AE平分∠BEF,连AF.
如图,点E,F分别为正方形ABCD的边BC、CD上一点,且AE平分∠BEF,连AF.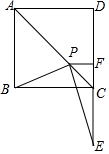 在正方形ABCD中,点P在对角线AC上,过点P作PF⊥CD于点F,作PE⊥PB交DC的延长线于点E,求证:DF=EF.
在正方形ABCD中,点P在对角线AC上,过点P作PF⊥CD于点F,作PE⊥PB交DC的延长线于点E,求证:DF=EF.