题目内容
11.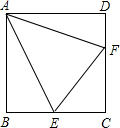 如图,点E,F分别为正方形ABCD的边BC、CD上一点,且AE平分∠BEF,连AF.
如图,点E,F分别为正方形ABCD的边BC、CD上一点,且AE平分∠BEF,连AF.(1)求证:∠EAF=45°;
(2)若点E为BC的中点,AB=6,求S△AEF.
分析 (1)作AH⊥EF于H.只要证明△AFD≌△AFH,推出∠FAD=∠FAH,同法可证:∠EAB=∠EAH,由此即可解决问题;
(2)由△EAB≌△EAH,△FAD≌△FAH,推出BE=EH=3,DF=FH,设DF=FH=x,在Rt△EFC中,根据EF2=EC2+CF2,可得(x+3)2=32+(6-x)2,推出x=2,推出EF=3+2=5,即可解决问题;
解答 (1)证明:作AH⊥EF于H.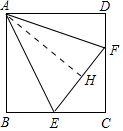
∵四边形ABCD是正方形,
∴∠B=∠D=∠BAD=90°,AB=AD=BC=CD,
∵AE平分∠BEF,AB⊥BE,AH⊥EF,
∴AB=AH=AD,
在Rt△AFD和Rt△AFH中,
$\left\{\begin{array}{l}{AF=AF}\\{AD=AH}\end{array}\right.$,
∴△AFD≌△AFH,
∴∠FAD=∠FAH,同法可证:∠EAB=∠EAH,
∴∠EAF=$\frac{1}{2}$∠BAH+$\frac{1}{2}$∠DAH=$\frac{1}{2}$×90°=45°.
(2)解:∵△EAB≌△EAH,△FAD≌△FAH,
∴BE=EH=3,DF=FH,设DF=FH=x,
在Rt△EFC中,∵EF2=EC2+CF2,
∴(x+3)2=32+(6-x)2,
∴x=2,
∴EF=3+2=5,
∴S△AEF=$\frac{1}{2}$×5×6=15.
点评 本题考查正方形的性质、全等三角形的判定和性质、角平分线的性质定理等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,属于中考常考题型.

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目
19.正方形网格中的图形①~④如图所示,其中图①、图②中的阴影三角形都有一个角是60°的直角三角形,图③、图④中阴影三角形都是有一个角是60°的锐角三角形,以上图形能围成正三棱柱的图形是( )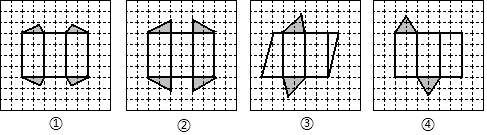

| A. | ①和④ | B. | ③和④ | C. | ①和② | D. | ②③④ |
20. 如图,将边长为4cm的正方形ABCD沿其对角线AC剪开,再把△ABC沿AD方向平移,得到△A′B′C′,若两个三角形重叠部分的面积是4cm2,则它移动的距离AA′等于( )
如图,将边长为4cm的正方形ABCD沿其对角线AC剪开,再把△ABC沿AD方向平移,得到△A′B′C′,若两个三角形重叠部分的面积是4cm2,则它移动的距离AA′等于( )
 如图,将边长为4cm的正方形ABCD沿其对角线AC剪开,再把△ABC沿AD方向平移,得到△A′B′C′,若两个三角形重叠部分的面积是4cm2,则它移动的距离AA′等于( )
如图,将边长为4cm的正方形ABCD沿其对角线AC剪开,再把△ABC沿AD方向平移,得到△A′B′C′,若两个三角形重叠部分的面积是4cm2,则它移动的距离AA′等于( )| A. | 3cm | B. | 2.5cm | C. | 1.5cm | D. | 2cm |
1.菱形ABCD的对角线AC=24,BD=10,则菱形的周长为( )
| A. | 20 | B. | 48 | C. | 52 | D. | 60 |
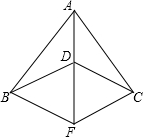 如图,已知AB=AC,DB=DC,F是AD的延长线上一点,求证:∠ABF=∠ACF.
如图,已知AB=AC,DB=DC,F是AD的延长线上一点,求证:∠ABF=∠ACF. 如图在Rt△ABC中,∠C=90°.CD是斜边AB上的高,若得到CD2=BD•AD这个结论可证明△ADC∽△CDB.
如图在Rt△ABC中,∠C=90°.CD是斜边AB上的高,若得到CD2=BD•AD这个结论可证明△ADC∽△CDB.