题目内容
5.如果把分式$\frac{{3n}^{2}}{m-n}$中的m和n都扩大3倍,那么分式的值( )| A. | 不变 | B. | 扩大3倍 | C. | 缩小3倍 | D. | 扩大9倍 |
分析 根据分式的性质,可得答案.
解答 解:把分式$\frac{{3n}^{2}}{m-n}$中的m和n都扩大3倍,得
$\frac{3(3n)^{2}}{3m-3n}$=$\frac{3×3n}{m-n}$,
故选:B.
点评 本题考查了分式的基本性质,把m,n分别换成3m,3n是解题关键.

练习册系列答案
相关题目
13. 圆锥的主视图如图所示(单位:cm),则这个圆锥的侧面积是( )
圆锥的主视图如图所示(单位:cm),则这个圆锥的侧面积是( )
 圆锥的主视图如图所示(单位:cm),则这个圆锥的侧面积是( )
圆锥的主视图如图所示(单位:cm),则这个圆锥的侧面积是( )| A. | 15cm2 | B. | 15πcm2 | C. | 30πcm2 | D. | 60cm2 |
20. 如图,将边长为4cm的正方形ABCD沿其对角线AC剪开,再把△ABC沿AD方向平移,得到△A′B′C′,若两个三角形重叠部分的面积是4cm2,则它移动的距离AA′等于( )
如图,将边长为4cm的正方形ABCD沿其对角线AC剪开,再把△ABC沿AD方向平移,得到△A′B′C′,若两个三角形重叠部分的面积是4cm2,则它移动的距离AA′等于( )
 如图,将边长为4cm的正方形ABCD沿其对角线AC剪开,再把△ABC沿AD方向平移,得到△A′B′C′,若两个三角形重叠部分的面积是4cm2,则它移动的距离AA′等于( )
如图,将边长为4cm的正方形ABCD沿其对角线AC剪开,再把△ABC沿AD方向平移,得到△A′B′C′,若两个三角形重叠部分的面积是4cm2,则它移动的距离AA′等于( )| A. | 3cm | B. | 2.5cm | C. | 1.5cm | D. | 2cm |
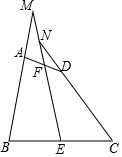 如图,在四边形ABCD中,AB=CD,E、F分别是BC、AD的中点,连结EF并延长,分别与BA,CD的延长线交于点M、N,证明:∠BME=∠CNE.
如图,在四边形ABCD中,AB=CD,E、F分别是BC、AD的中点,连结EF并延长,分别与BA,CD的延长线交于点M、N,证明:∠BME=∠CNE.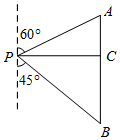 如图,小明同学在点P处测得教学楼A位于北偏东60°方向,办公楼B位于南偏东45°方向.小明沿正东方向前进60米到达C处,此时测得教学楼A恰好位于正北方向.办公楼B正好位于正南方向.求教学楼A与办公楼B之间的距离(60+20$\sqrt{3}$)米.
如图,小明同学在点P处测得教学楼A位于北偏东60°方向,办公楼B位于南偏东45°方向.小明沿正东方向前进60米到达C处,此时测得教学楼A恰好位于正北方向.办公楼B正好位于正南方向.求教学楼A与办公楼B之间的距离(60+20$\sqrt{3}$)米.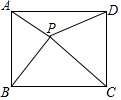 如图,点P是矩形ABCD内一点,连接PA、PB、PC、PD,已知AB=3,BC=4,设△PAB、△PBC、△PDA的面积分别为S1、S2、S3、S4,以下判断:
如图,点P是矩形ABCD内一点,连接PA、PB、PC、PD,已知AB=3,BC=4,设△PAB、△PBC、△PDA的面积分别为S1、S2、S3、S4,以下判断: