题目内容
4.在Rt△ABC中,∠C=90°,AC=4,BC=3,则sinB的值等于$\frac{4}{5}$.分析 直接利用勾股定理得出AB的长,再利用锐角三角函数关系得出答案.
解答 解:∵在Rt△ABC中,∠C=90°,AC=4,BC=3,
∴AB=5,
∴sinB=$\frac{AC}{AB}$=$\frac{4}{5}$.
故答案为:$\frac{4}{5}$.
点评 此题主要考查了锐角三角函数关系,正确记忆边角关系是解题关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
19.正方形网格中的图形①~④如图所示,其中图①、图②中的阴影三角形都有一个角是60°的直角三角形,图③、图④中阴影三角形都是有一个角是60°的锐角三角形,以上图形能围成正三棱柱的图形是( )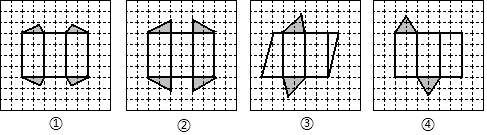

| A. | ①和④ | B. | ③和④ | C. | ①和② | D. | ②③④ |
13. 圆锥的主视图如图所示(单位:cm),则这个圆锥的侧面积是( )
圆锥的主视图如图所示(单位:cm),则这个圆锥的侧面积是( )
 圆锥的主视图如图所示(单位:cm),则这个圆锥的侧面积是( )
圆锥的主视图如图所示(单位:cm),则这个圆锥的侧面积是( )| A. | 15cm2 | B. | 15πcm2 | C. | 30πcm2 | D. | 60cm2 |
 由于近年来电力紧缺,某省电力公司为鼓励市民节约用电,采取按月用电量分段收费办法.若某户居民每月应交电费y(元)与用电量x(度)的函数图象是一条折线(如图所示),根据图象解下列问题:
由于近年来电力紧缺,某省电力公司为鼓励市民节约用电,采取按月用电量分段收费办法.若某户居民每月应交电费y(元)与用电量x(度)的函数图象是一条折线(如图所示),根据图象解下列问题: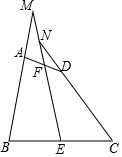 如图,在四边形ABCD中,AB=CD,E、F分别是BC、AD的中点,连结EF并延长,分别与BA,CD的延长线交于点M、N,证明:∠BME=∠CNE.
如图,在四边形ABCD中,AB=CD,E、F分别是BC、AD的中点,连结EF并延长,分别与BA,CD的延长线交于点M、N,证明:∠BME=∠CNE.