题目内容
4.已知方程组$\left\{\begin{array}{l}{y=x+1}\\{y=2x-3}\end{array}\right.$的解为$\left\{\begin{array}{l}{x=4}\\{y=5}\end{array}\right.$,直线y=x+1与直线y=2x-3的交点坐标是( )| A. | (4,5) | B. | (5,4) | C. | (4,0) | D. | (5,0) |
分析 二元一次方程组的解就是两个一次函数图象的交点.
解答 解:∵方程组$\left\{\begin{array}{l}{y=x+1}\\{y=2x-3}\end{array}\right.$的解为$\left\{\begin{array}{l}{x=4}\\{y=5}\end{array}\right.$,
∴直线y=x+1与直线y=2x-3的交点坐标是(4,5).
故选A.
点评 此题主要考查了一次函数与二元一次方程组的解,关键是掌握二者之间的关系.

练习册系列答案
相关题目
16.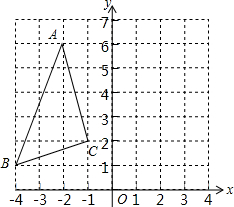 如图,如果将△ABC先向右平移1个单位长度,再绕原点O顺时针旋转90°,得到△A1B1C1,那么点A的对应点A1的坐标为( )
如图,如果将△ABC先向右平移1个单位长度,再绕原点O顺时针旋转90°,得到△A1B1C1,那么点A的对应点A1的坐标为( )
 如图,如果将△ABC先向右平移1个单位长度,再绕原点O顺时针旋转90°,得到△A1B1C1,那么点A的对应点A1的坐标为( )
如图,如果将△ABC先向右平移1个单位长度,再绕原点O顺时针旋转90°,得到△A1B1C1,那么点A的对应点A1的坐标为( )| A. | (1,3) | B. | (2,0) | C. | (6,1) | D. | (6,2) |
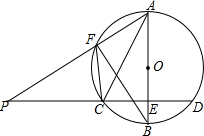 如图,AB是⊙O的直径,AC是弦,点P在⊙O外,连接PA交⊙O于点F,连接PC并延长交⊙O于点D,交AB于点E,连接FC、FB,若AC2=AF•AP,AC=4$\sqrt{5}$,CD=8,求⊙O的半径.
如图,AB是⊙O的直径,AC是弦,点P在⊙O外,连接PA交⊙O于点F,连接PC并延长交⊙O于点D,交AB于点E,连接FC、FB,若AC2=AF•AP,AC=4$\sqrt{5}$,CD=8,求⊙O的半径.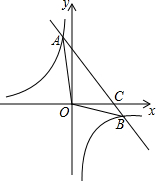 如图,已知一次函数y=ax+b的图象与反比例函数y=$\frac{k}{x}$的图象相交于点A(-2,m)和点B(4,-2),与x轴交于点C
如图,已知一次函数y=ax+b的图象与反比例函数y=$\frac{k}{x}$的图象相交于点A(-2,m)和点B(4,-2),与x轴交于点C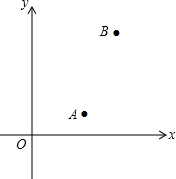 如图,已知A,B两村庄在平面直角坐标系中的坐标分别为(3,1),(5,5),若长途客车沿y轴行驶到P处时,与A,B两村庄的距离之和最小,则点P的坐标为(0,$\frac{5}{2}$).
如图,已知A,B两村庄在平面直角坐标系中的坐标分别为(3,1),(5,5),若长途客车沿y轴行驶到P处时,与A,B两村庄的距离之和最小,则点P的坐标为(0,$\frac{5}{2}$).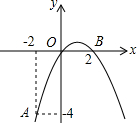 如图,抛物线y=ax2+bx+c经过A(-2,-4),O(0,0),B(2、0)三点.
如图,抛物线y=ax2+bx+c经过A(-2,-4),O(0,0),B(2、0)三点.