题目内容
11.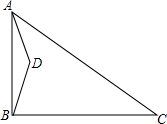 在△ABC中,∠ABC=90°,D为平面内一动点,AD=a,AC=b,其中a,b为常数,且a<b.将△ABD沿射线BC方向平移,得到△FCE,点A、B、D的对应点分别为点F、C、E.连接BE.
在△ABC中,∠ABC=90°,D为平面内一动点,AD=a,AC=b,其中a,b为常数,且a<b.将△ABD沿射线BC方向平移,得到△FCE,点A、B、D的对应点分别为点F、C、E.连接BE.(1)如图,若D在△ABC内部,请在图中画出△FCE;
(2)在(1)的条件下,若AD⊥BE,求BE的长(用含a,b的式子表示).
分析 (1)把A、D向右平移BC的距离即可得到对应点F、E,然后连接EF、FC、EC即可;
(2)易证四边形ABCF为矩形,则AC=BF,在直角△BEF中,利用勾股定理即可求解.
解答 解:(1)如图,
(2)连接BE、BF.
∵将△ABD沿射线BC方向平移,得到△FCE,
∴AD∥EF,AD=EF;AB∥FC,AB=FC.
∵∠ABC=90°,
∴四边形ABCF为矩形,
∴AC=BF.
∵AD⊥BE,
∴EF⊥BE.
∵AD=a,AC=b,
∴EF=a,BF=b.
∴BE=$\sqrt{{b}^{2}-{a}^{2}}$.
点评 本题考查了作图-平移变换,矩形的判定与性质以及勾股定理,掌握图形平移后边的大小,形状不变是解题的关键.

练习册系列答案
相关题目
20.2010年3月份,某市市区一周空气质量报告中某项污染指数的数据是:31,35,31,34,30,32,31,这组数据的中位数、众数分别是( )
| A. | 32,31 | B. | 31,32 | C. | 31,31 | D. | 32,35 |
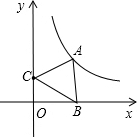 如图,点A是反比例函数y=$\frac{5\sqrt{3}}{x}$(x>0)图象上一点,点B是x轴正半轴上一点,点C的坐标为(0,2),当△ABC是等边三角形时,点A的坐标为($\frac{3\sqrt{3}}{5}$,$\frac{25}{3}$).
如图,点A是反比例函数y=$\frac{5\sqrt{3}}{x}$(x>0)图象上一点,点B是x轴正半轴上一点,点C的坐标为(0,2),当△ABC是等边三角形时,点A的坐标为($\frac{3\sqrt{3}}{5}$,$\frac{25}{3}$).
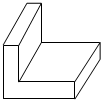 一个用于防震的L形包装塑料泡沫如图所示,则该物体的俯视图是( )
一个用于防震的L形包装塑料泡沫如图所示,则该物体的俯视图是( )