题目内容
11.若圆锥的底面半径为3,母线长为4,则这个圆锥的侧面积为 ( )| A. | 12π | B. | 21π | C. | 24π | D. | 42π |
分析 圆锥的侧面积=底面周长×母线长÷2,把相应数值代入即可求解.
解答 解:圆锥的侧面积=2π×3×4÷2=12π.
故选A.
点评 本题考查了圆锥的计算,解题的关键是弄清圆锥的侧面积的计算方法,特别是圆锥的底面周长等于圆锥的侧面扇形的弧长.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
1.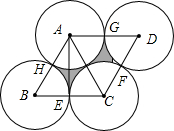 如图,菱形ABCD的边长为2,且AE⊥BC,E、F、G、H分别为BC、CD、DA、AB的中点,以A、B、C、D四点为圆心,半径为1作圆,则图中阴影部分的面积是( )
如图,菱形ABCD的边长为2,且AE⊥BC,E、F、G、H分别为BC、CD、DA、AB的中点,以A、B、C、D四点为圆心,半径为1作圆,则图中阴影部分的面积是( )
 如图,菱形ABCD的边长为2,且AE⊥BC,E、F、G、H分别为BC、CD、DA、AB的中点,以A、B、C、D四点为圆心,半径为1作圆,则图中阴影部分的面积是( )
如图,菱形ABCD的边长为2,且AE⊥BC,E、F、G、H分别为BC、CD、DA、AB的中点,以A、B、C、D四点为圆心,半径为1作圆,则图中阴影部分的面积是( )| A. | $\sqrt{3}$-π | B. | $\sqrt{3}$-2π | C. | 2$\sqrt{3}$-π | D. | 2$\sqrt{3}$-2π |
19.如果关于x的方程ax2+4x-2=0有两个不相等的实数根,且关于x的分式方程$\frac{1}{2-x}$-$\frac{1-ax}{x-2}$=2有正数解,则符合条件的整数a的值是( )
| A. | -1 | B. | 0 | C. | 1 | D. | 2 |
6.反比例函数$y=-\frac{6}{x}$图象上有三个点(x1,y1),(x2,y2),(x3,y3),其中x1<x2<0<x3,则y1,y2,y3的大小关系是( )
| A. | y1<y2<y3 | B. | y2<y1<y3 | C. | y3<y1<y2 | D. | y3<y2<y1 |
16.如果一个角的补角是120°则这个角的余角的度数是( )
| A. | 30° | B. | 60° | C. | 90° | D. | 120° |
3.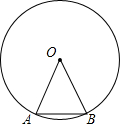 如图边长为2的正三角形OAB的顶点A、B在一个半径为2的圆上,将正三角形OAB沿圆的内壁作无滑动的滚动.当滚动一周回到原位置时,点B运动的路径长为( )
如图边长为2的正三角形OAB的顶点A、B在一个半径为2的圆上,将正三角形OAB沿圆的内壁作无滑动的滚动.当滚动一周回到原位置时,点B运动的路径长为( )
 如图边长为2的正三角形OAB的顶点A、B在一个半径为2的圆上,将正三角形OAB沿圆的内壁作无滑动的滚动.当滚动一周回到原位置时,点B运动的路径长为( )
如图边长为2的正三角形OAB的顶点A、B在一个半径为2的圆上,将正三角形OAB沿圆的内壁作无滑动的滚动.当滚动一周回到原位置时,点B运动的路径长为( )| A. | 4π | B. | 2π | C. | $\frac{10}{3}$π | D. | $\frac{8}{3}$π |
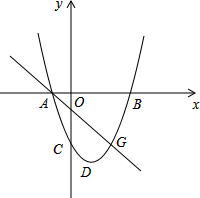 如图,在平面直角坐标系中,二次函数y=ax2+bx+c(a>0)的图象的顶点为D,与y轴交于点C,与x轴交于A、B两点,点A在原点的左侧,点B的坐标为(3,0),OB=OC=3OA.
如图,在平面直角坐标系中,二次函数y=ax2+bx+c(a>0)的图象的顶点为D,与y轴交于点C,与x轴交于A、B两点,点A在原点的左侧,点B的坐标为(3,0),OB=OC=3OA.


