如图边长为2的正三角形OAB的顶点A.B在一个半径为2的圆上.将正三角形OAB沿圆的内壁作无滑动的滚动．当滚动一周回到原位置时.点B运动的路径长为( )A．4πB．2πC．$\frac{10}{3}$πD．$\frac{8}{3}$π 题目和参考答案——青夏教育精英家教网—

题目内容

3．

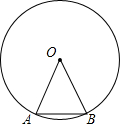如图边长为2的正三角形OAB的顶点A、B在一个半径为2的圆上，将正三角形OAB沿圆的内壁作无滑动的滚动．当滚动一周回到原位置时，点B运动的路径长为（　　）

A．

4π

B．

2π

C．

$\frac{10}{3}$π

D．

$\frac{8}{3}$π

分析首先判断出当滚动一周回到原位置时点B滚动四次，每次滚动的弧长是圆心角为60°半径为2的弧长，由此即可解决问题．

解答解：如图，正三角形OAB沿圆的内壁作无滑动的滚动，当滚动一周回到原位置时，
点B滚动四次，每次滚动的弧长是圆心角为60°半径为2的弧长，
∴点B运动的路径长=4×$\frac{60π•2}{180}$=$\frac{8}{3}$π．
故答案为$\frac{8}{3}$π．

点评本题考查轨迹、等边三角形、弧长公式等知识，解题的关键是理解题意，正确判断点B的滚动情形，记住弧长公式=$\frac{nπR}{180}$，属于中考常考题型．

练习册系列答案

14．在平面直角坐标系xOy中，抛物线C：y=ax²．
（1）若直线l₁：y=x-1与抛物线C有且只有1个交点，求抛物线C的解析式．
（2）如图1，在（1）的条件下，在y轴上有一点A（0，4），过点A作直线l₂与抛物线C有两个交点M、N（N位于第一象限），过点N作x轴的垂线，垂足为H．试探究：是否存在l₂，使△MON∽△NHO？若存在，求出l₂的解析式；若不存在，说明理由．
（3）如图2，E、F为抛物线C（y=ax²）上两动点，始终满足OE⊥OF，连接EF，则直线EF是否恒过一定点G？若存在点G，直接写出G点坐标（用含a的坐标表示），若不存在，给予证明．
（参考结论：若直线l：y=kx+b上有两点（x₁，y₁）、（x₂，y₂），则斜率k=$\frac{{y}_{2}-{y}_{1}}{{x}_{2}-{x}_{1}}$；当两直线l₁、l₂的斜率乘积k₁•k₂=-1时，l₁⊥l₂）

11．若圆锥的底面半径为3，母线长为4，则这个圆锥的侧面积为（　　）

8．如图1，在平面直角坐标系中，点A的坐标是（3，4），点B在x轴的正半轴上，∠ABO=45°，过点A作AC⊥y轴于点C，过点B作直线l∥y轴．
（1）求B点的坐标；
（2）如图2，动点P从点O出发，以每秒1个单位长度的速度，沿O-C-A的路线向点A运动，同时直线l从点B出发，以相同速度向左平移，在平移过程中，直线l交x轴于点D，交线段BA或线段AO于点E，当点P到达点A时，点P和直线l都停止运动，设点P的运动时间为ts．
①求△PAD的面积S与t之间的函数关系式；
②当t为何值时，S=8？
③点P在CA上运动时，是否存在以点A为圆心，AE长为半径的⊙A与坐标轴相切？如果存在，求出t的值；如果不存在，请说明理由．

a³•a²=a⁶

12．若关于x的分式方程$\frac{m}{x-2}$+$\frac{x+1}{2-x}$=3有增根，则m的值是（　　）

a²+a³=a⁵

（a²）³=a⁵

a⁶÷a²=a⁴

试题分类