题目内容
6.反比例函数$y=-\frac{6}{x}$图象上有三个点(x1,y1),(x2,y2),(x3,y3),其中x1<x2<0<x3,则y1,y2,y3的大小关系是( )| A. | y1<y2<y3 | B. | y2<y1<y3 | C. | y3<y1<y2 | D. | y3<y2<y1 |
分析 先根据反比例函数的解析式判断出其函数图象所在的象限,再根据x1<x2<0<x3,判断出各点横坐标的大小即可.
解答 解:∵反比例函数$y=-\frac{6}{x}$中,k=-6<0,
∴函数图象的两个分支分别位于二四象限,且在每一象限内y随x的增大而增大.
∵x1<x2<0<x3,
∴(x1,y1),(x2,y2)两点位于第二象限,点(x3,y3)位于第四象限,
∴y3<y1<y2.
故选C.
点评 本题考查的是反比例函数图象上点的坐标特点,熟知反比例函数的增减性是解答此题的关键.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
16. 一个不等式的解集在数轴上表示如图所示,则这个不等式可能是( )
一个不等式的解集在数轴上表示如图所示,则这个不等式可能是( )
 一个不等式的解集在数轴上表示如图所示,则这个不等式可能是( )
一个不等式的解集在数轴上表示如图所示,则这个不等式可能是( )| A. | x>-1 | B. | x≥-1 | C. | x<-1 | D. | x≤-1 |
17.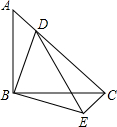 如图,等腰Rt△ABC中,BA=BC,∠ABC=90°,点D在AC上,将△ABD绕点B沿顺时针方向旋转90°后,得到△CBE.
如图,等腰Rt△ABC中,BA=BC,∠ABC=90°,点D在AC上,将△ABD绕点B沿顺时针方向旋转90°后,得到△CBE.
(1)求∠DCE的度数;
(2)若AB=4,CD=3AD,求DE的长.
 如图,等腰Rt△ABC中,BA=BC,∠ABC=90°,点D在AC上,将△ABD绕点B沿顺时针方向旋转90°后,得到△CBE.
如图,等腰Rt△ABC中,BA=BC,∠ABC=90°,点D在AC上,将△ABD绕点B沿顺时针方向旋转90°后,得到△CBE.(1)求∠DCE的度数;
(2)若AB=4,CD=3AD,求DE的长.
1. O为△ABC外心,∠BOC=40°,则∠BAC=( )
O为△ABC外心,∠BOC=40°,则∠BAC=( )
 O为△ABC外心,∠BOC=40°,则∠BAC=( )
O为△ABC外心,∠BOC=40°,则∠BAC=( )| A. | 40° | B. | 30° | C. | 20° | D. | 10° |
11.若圆锥的底面半径为3,母线长为4,则这个圆锥的侧面积为 ( )
| A. | 12π | B. | 21π | C. | 24π | D. | 42π |
18.下列四个数中,最小的数是( )
| A. | 1 | B. | 0 | C. | -3 | D. | -$\sqrt{5}$ |
15.下列运算正确的是( )
| A. | a+2b=3ab | B. | a3•a2=a6 | C. | a3÷a3=a | D. | (5a)2=25a2 |
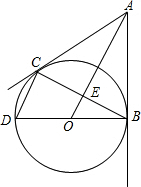 如图,AB,AC分别切⊙O于B,C,⊙O的直径BD=6,连接CD,AO,BC.AO与BC相交于点E.
如图,AB,AC分别切⊙O于B,C,⊙O的直径BD=6,连接CD,AO,BC.AO与BC相交于点E.