题目内容
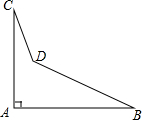 一个零件的形状如图,按规定∠A应等于90°,∠B与∠C应分别是32°和21°,检验工人量得∠BDC=148°,就判断这个零件不合格,试用三角形的有关知识说明理由.
一个零件的形状如图,按规定∠A应等于90°,∠B与∠C应分别是32°和21°,检验工人量得∠BDC=148°,就判断这个零件不合格,试用三角形的有关知识说明理由.考点:三角形的外角性质
专题:应用题
分析:延长CD交AB于E,根据三角形的一个外角等于与它不相邻的两个内角的和列式求出∠BDC,然后即可判断.
解答:解:如图,

延长CD交AB于E,
∵∠A=90°,∠C=21°,
∴∠1=∠A+∠C=90°+21°=111°,
∵∠B=32°,
∴∠BDC=∠B+∠1=32°+111°=143°.
又∵∠BDC=148°,
∴这个零件不合格.

延长CD交AB于E,
∵∠A=90°,∠C=21°,
∴∠1=∠A+∠C=90°+21°=111°,
∵∠B=32°,
∴∠BDC=∠B+∠1=32°+111°=143°.
又∵∠BDC=148°,
∴这个零件不合格.
点评:本题考查的是三角形外角的性质,根据题意作出辅助线,构造出三角形,利用三角形外角的性质求解是解答此题的关键.

练习册系列答案
相关题目
根据如图所示的程序,若输入的自变量x的值为-1,则输出的因变量y的值为( )


| A、1 | ||
| B、-2 | ||
C、
| ||
| D、3 |
若x=-2,则|x-3|的值是( )
| A、1 | B、-1 | C、5 | D、-5 |
 如图,△ABC中,∠C>∠B,AE为角平分线,AD⊥BC于D.
如图,△ABC中,∠C>∠B,AE为角平分线,AD⊥BC于D. 如图,AD是等腰△ABC的顶角平分线,E、F分别是DC、AB上的点,求作点E、F关于
如图,AD是等腰△ABC的顶角平分线,E、F分别是DC、AB上的点,求作点E、F关于 如图是某产品的商标图案,求阴影部分的面积.
如图是某产品的商标图案,求阴影部分的面积.