题目内容
矩形ABCD中,对角线AC、BD相交于点O,∠AOB=2∠BOC,若AC=18cm,则AB= cm.
考点:矩形的性质,勾股定理
专题:
分析:由条件可先求得∠AOB=120°,结合矩形的性质可得∠BAC=30°,在Rt△ABC中由勾股定理可求得AB.
解答: 解:如图,
解:如图,
∵∠AOB+∠BOC=180°且∠AOB=2∠BOC,
∴∠AOB=120°,
又∵四边形ABCD为矩形,
∴OA=OB,且∠ABC=90°,
∴∠OAB=
=30°,
∴BC=
AC=9cm,
在Rt△ABC中,由勾股定理可求得AB=9
cm,
故答案为:9
.
 解:如图,
解:如图,∵∠AOB+∠BOC=180°且∠AOB=2∠BOC,
∴∠AOB=120°,
又∵四边形ABCD为矩形,
∴OA=OB,且∠ABC=90°,
∴∠OAB=
| 180°-120° |
| 2 |
∴BC=
| 1 |
| 2 |
在Rt△ABC中,由勾股定理可求得AB=9
| 3 |
故答案为:9
| 3 |
点评:本题主要考查矩形的性质,掌握矩形的对边相等、每个角为直角、对角线相等且平分是解题的关键.

练习册系列答案
 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
 如图,AD=BD=CD,∠CBD=20°,则∠BAC=( )
如图,AD=BD=CD,∠CBD=20°,则∠BAC=( )| A、40° | B、60° |
| C、70° | D、80° |
互为余角的两个角之比是2:3,则这两个角分别是( )
| A、72°,108° |
| B、38°,52° |
| C、40°,60° |
| D、36°,54° |
若x=-2,则|x-3|的值是( )
| A、1 | B、-1 | C、5 | D、-5 |
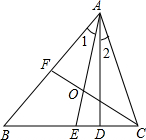 如图,△ABC中,∠C>∠B,AE为角平分线,AD⊥BC于D.
如图,△ABC中,∠C>∠B,AE为角平分线,AD⊥BC于D. 如图,在某海岛上的观察所A测得海上某船只B的俯角α=8°18′,若观察所A与船只B的水平距离BC等于100米,则海岛高AC为
如图,在某海岛上的观察所A测得海上某船只B的俯角α=8°18′,若观察所A与船只B的水平距离BC等于100米,则海岛高AC为 如图,在△ABC的顶点A的直线上取两点D、E,连接BD、CE,已知∠1=∠2,∠3=∠4,∠5=∠6;求证:BD∥AC.
如图,在△ABC的顶点A的直线上取两点D、E,连接BD、CE,已知∠1=∠2,∠3=∠4,∠5=∠6;求证:BD∥AC.