题目内容
用配方法求函数y=
x-2-3x2的最大值或最小值.
| 4 |
| 3 |
考点:二次函数的最值
专题:
分析:直接将所给的二次函数配方,即可解决问题.
解答:解:∵y=
x-2-3x2,
∴y=-3(x-
)2-
,
∵a=-3<0,
∴抛物线y=
x-2-3x2开口向上,
函数y有最小值,ymin=-
.
| 4 |
| 3 |
∴y=-3(x-
| 2 |
| 9 |
| 50 |
| 27 |
∵a=-3<0,
∴抛物线y=
| 4 |
| 3 |
函数y有最小值,ymin=-
| 50 |
| 27 |
点评:该题主要考查了用配方法来求二次函数的最值问题;解题的关键是准确配方,正确求值.

练习册系列答案
相关题目
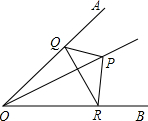 如图,∠AOB=45°,角内有一点P,PO=10,在角两边上有两点Q、R(均不同于点O),则△PQR的周长最小值是
如图,∠AOB=45°,角内有一点P,PO=10,在角两边上有两点Q、R(均不同于点O),则△PQR的周长最小值是