题目内容
二次函数y=2(x-m)2+4,当m<-
时,y随x的增大而减小;当x>-
时,y随x的增大而增大,当x=-
时,函数y的值是多少?当x=1时,函数y的值是多少?
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
考点:二次函数的性质
专题:计算题
分析:根据二次函数的性质得抛物线的对称轴为直线x=-
,则利用顶点式即可得到m=-
,所以抛物线解析式为y=2(x+
)2+4,然后分别计算x=-
和1的函数值即可.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:∵当m<-
时,y随x的增大而减小;当x>-
时,y随x的增大而增大,
∴抛物线的对称轴为直线x=-
,
∴m=-
,
∴抛物线解析式为y=2(x+
)2+4,
∴当x=-
时,y=y=2(x+
)2+4=4,
当x=1时,y=2(x+
)2+4=2•
+4=
即当x=-
时,函数y的值是4;当x=1时,函数y的值是
.
| 1 |
| 2 |
| 1 |
| 2 |
∴抛物线的对称轴为直线x=-
| 1 |
| 2 |
∴m=-
| 1 |
| 2 |
∴抛物线解析式为y=2(x+
| 1 |
| 2 |
∴当x=-
| 1 |
| 2 |
| 1 |
| 2 |
当x=1时,y=2(x+
| 1 |
| 2 |
| 9 |
| 4 |
| 17 |
| 2 |
即当x=-
| 1 |
| 2 |
| 17 |
| 2 |
点评:本题考查了二次函数的性质:二次函数y=ax2+bx+c(a≠0)的顶点坐标是(-
,
),对称轴直线x=-
,二次函数y=ax2+bx+c(a≠0)的图象具有如下性质:当a>0时,抛物线y=ax2+bx+c(a≠0)的开口向上,x<-
时,y随x的增大而减小;x>-
时,y随x的增大而增大;x=-
时,y取得最小值
,即顶点是抛物线的最低点.当a<0时,抛物线y=ax2+bx+c(a≠0)的开口向下,x<-
时,y随x的增大而增大;x>-
时,y随x的增大而减小;x=-
时,y取得最大值
,即顶点是抛物线的最高点.
| b |
| 2a |
| 4ac-b2 |
| 4a |
| b |
| 2a |
| b |
| 2a |
| b |
| 2a |
| b |
| 2a |
| 4ac-b2 |
| 4a |
| b |
| 2a |
| b |
| 2a |
| b |
| 2a |
| 4ac-b2 |
| 4a |

练习册系列答案
相关题目
“六一”期间,某商店将单价标为130元的书包按8折出售可获利30%,该书包每个的进价是( )
| A、65元 | B、80元 |
| C、100元 | D、104元 |
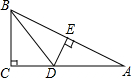 如图,在Rt△ABC中,∠C=90°,AB的垂直平分线交AC于点D,交AB于点E.若BC=2,AC=4,则BD=( )
如图,在Rt△ABC中,∠C=90°,AB的垂直平分线交AC于点D,交AB于点E.若BC=2,AC=4,则BD=( )A、
| ||
| B、2 | ||
C、
| ||
| D、3 |
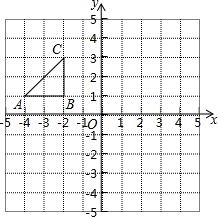 在平面直角坐标系中,△ABC的顶点坐标A(-4,1),B(-2,1),C(-2,3)
在平面直角坐标系中,△ABC的顶点坐标A(-4,1),B(-2,1),C(-2,3)