题目内容
2.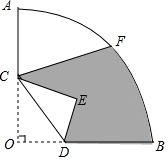 如图,在圆心角为90°的扇形AOB中,半径OA=3,OC=AC,OD=$\frac{1}{2}$BD,F是弧AB的中点.将△OCD沿CD折叠,点O落在点E处,则图中阴影部分的面积为$\frac{9π+9\sqrt{2}-12}{8}$.
如图,在圆心角为90°的扇形AOB中,半径OA=3,OC=AC,OD=$\frac{1}{2}$BD,F是弧AB的中点.将△OCD沿CD折叠,点O落在点E处,则图中阴影部分的面积为$\frac{9π+9\sqrt{2}-12}{8}$.
分析 连接OF,过C作CH⊥OF于H,根据已知条件得到OC=1.5,OD=2,由F是弧AB的中点.得到∠COH=45°,根据图形的面积即可得到结论.
解答 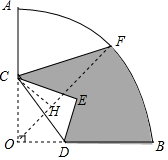 解:连接OF,过C作CH⊥OF于H,
解:连接OF,过C作CH⊥OF于H,
∵OA=OB=OF=3,OC=AC,OD=$\frac{1}{2}$BD,
∴OC=1.5,OD=2,
∵F是弧AB的中点.
∴∠COH=45°,
∴CH=OH=$\frac{3\sqrt{2}}{4}$,
∴S阴影=S扇形FOB+S△COF-2S△COD=$\frac{45•π×{3}^{2}}{360}$+$\frac{1}{2}×$3×$\frac{3\sqrt{2}}{4}$-2×$\frac{1}{2}$×$\frac{3}{2}$×1=$\frac{9π+9\sqrt{2}-12}{8}$,
故答案为:$\frac{9π+9\sqrt{2}-12}{8}$.
点评 本题考查了扇形的面积的计算,折叠的性质,正确的作出辅助线是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.已知a.b,C是三角形的三边,那么代数式a2-2ab+b2-c2的值( )
| A. | 小于零 | B. | 等于零 | C. | 大于零 | D. | 不能确定 |
12.$\sqrt{13}$≈3.61,$\sqrt{1.3}$≈1.14,则$\sqrt{13000}$≈( )
| A. | 36.1 | B. | 11.4 | C. | 361 | D. | 114 |
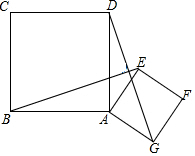 如图,已知正方形ABCD和正方形AEFG,连结BE、DG.
如图,已知正方形ABCD和正方形AEFG,连结BE、DG.