Question

3．如图，四边形ABCD中，∠BAD=60°，∠BCD=30°，AB=AD，求证：BC²+CD²=AC²．

Answer 1

分析 将△ADC以A为旋转中心，顺时针旋转60°，使D与B点重合，C与E点重合，连接CE，根据旋转的性质得∠ACD=∠AEB，∠D=∠EBA，DC=BE，AE=AC，易得△AEC为等边三角形，则AC=CE，根据周角的定义和四边形内角和定理得∠EBC=360°-∠CBA-∠ABE=360°-∠CBA-∠D=360°-（360°-∠DAB-∠DCB）=60°+30°=90°，则△EBC为直角三角形，根据勾股定理得EB²+BC²=CE²，利用等线段代换即可得到结论．

解答 证明：如图，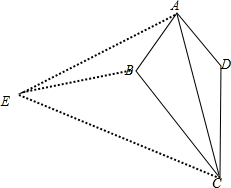

将△DAC以A为旋转中心，顺时针旋转60°，使D与B点重合，C与E点重合，连接CE，
∴∠DCA=∠BEA，∠D=∠EBA，DC=BE，AC=AE，
又∵∠DAB=60°，
∴∠CAE=60°，
∴△ACE为等边三角形，
∴AC=CE，
又∴∠EBC=360°-∠CBA-∠ABE
=360°-∠CBA-∠D
=360°-（360°-∠DAB-∠DCB）
=60°+30°
=90°，
∴△EBC为直角三角形，
∴EB²+BC²=CE²，
∴AC²=CD²+BC²．

点评 本题考查了旋转的性质：旋转前后两图形全等，即对应角相等，对应线段相等，对应点与旋转中心的连线段的夹角等于旋转角．也考查了全等三角形的判定与性质、等边三角形的判定与性质以及勾股定理．