题目内容
如下三图中,已知A(0,10)、B(10,0),P是线段AB的中点.
(1)S△AOB= ,P点的坐标是 ;
(2)如图2,C(-4,0),D为y轴上的一点,当△PDC是以P为顶点的等腰直角三角形时,求D点的坐标;
(3)如图3,当等腰直角△PCD绕P点在线段AB左下方转动时,记△PCD与△AOB重叠部分即图中阴影四边形PMON的面积为S,S的值是否为定值?如是定值,求其值;如是变化的,说明是怎样变化.
(1)S△AOB=
(2)如图2,C(-4,0),D为y轴上的一点,当△PDC是以P为顶点的等腰直角三角形时,求D点的坐标;
(3)如图3,当等腰直角△PCD绕P点在线段AB左下方转动时,记△PCD与△AOB重叠部分即图中阴影四边形PMON的面积为S,S的值是否为定值?如是定值,求其值;如是变化的,说明是怎样变化.

考点:全等三角形的判定与性质,坐标与图形性质,等腰直角三角形
专题:
分析:(1)根据A、B坐标求出OA、OB,即可求出答案;
(2)作PE⊥OB于E,PF⊥OA于F,证三角形PCE和三角形PDF全等,即可求出答案;
(3)连接OP,证△PON≌△PBM,推出S△PON=S△PBM,即可求出阴影部分的面积等于三角形AOB面积的一半,求出即可.
(2)作PE⊥OB于E,PF⊥OA于F,证三角形PCE和三角形PDF全等,即可求出答案;
(3)连接OP,证△PON≌△PBM,推出S△PON=S△PBM,即可求出阴影部分的面积等于三角形AOB面积的一半,求出即可.
解答:解:(1)∵A(0,10)、B(10,0),
∴OA=OB=10,
∴S△AOB=
×OA×OB=
×10×10=50,
作PE⊥OB于E,PF⊥OA于F,如图1,
∵P是线段AB的中点,
∴PE=PF=5,
P(5,5),
故答案为:50,(5,5);
(2)如图1,作PE⊥OB于E,PF⊥OA于F,
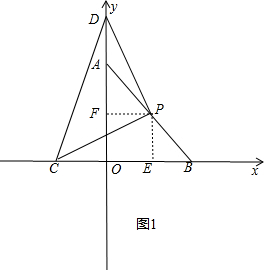
∵P是线段AB的中点,
∴PE=PF=5,CE=CO+OE=4+5=9,
∵△PCD是等腰直角三角形,
在△PCE和△PDF中,
∴Rt△PCE≌Rt△PDF(HL),
∴CE=DF=9,
∴OF=5,
∴OD=OF+DF=5+9=14,
∴D(0,14);
(3)S的值是定值,
如图2,连接OP,
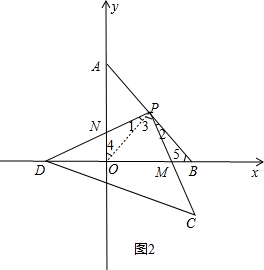
∵P是线段AB的中点,OA=OB
∴△POA与△POB均是等腰直角三形,
∴PO=PB,∠4=∠5=45°
∵∠1+∠3=∠3+∠2=90°,
∴∠1=∠2,
在△PON和△PBM中,
,
∴△PON≌△PBM(ASA),
∴S△PON=S△PBM,
∴S四边形PMON=S△PON+S△POM=S△PBM+S△POM=S△POB=
S△AOB=25.
∴OA=OB=10,
∴S△AOB=
| 1 |
| 2 |
| 1 |
| 2 |
作PE⊥OB于E,PF⊥OA于F,如图1,
∵P是线段AB的中点,
∴PE=PF=5,
P(5,5),
故答案为:50,(5,5);
(2)如图1,作PE⊥OB于E,PF⊥OA于F,

∵P是线段AB的中点,
∴PE=PF=5,CE=CO+OE=4+5=9,
∵△PCD是等腰直角三角形,
在△PCE和△PDF中,
|
∴Rt△PCE≌Rt△PDF(HL),
∴CE=DF=9,
∴OF=5,
∴OD=OF+DF=5+9=14,
∴D(0,14);
(3)S的值是定值,
如图2,连接OP,

∵P是线段AB的中点,OA=OB
∴△POA与△POB均是等腰直角三形,
∴PO=PB,∠4=∠5=45°
∵∠1+∠3=∠3+∠2=90°,
∴∠1=∠2,
在△PON和△PBM中,
|
∴△PON≌△PBM(ASA),
∴S△PON=S△PBM,
∴S四边形PMON=S△PON+S△POM=S△PBM+S△POM=S△POB=
| 1 |
| 2 |
点评:本题考查了点的坐标与图形面积,直角三角形的性质,全等三角形的性质和判定的应用,主要考查学生的推理能力,题目比较好,难度适中.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
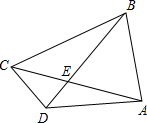 如图所示,已知四边形ABCD的对角线AC、BD相交于点E,△AED∽△BEC,其中A、E、D三点的对应点分别为B、E、C三点,∠ADE=∠ACD,若△ABE的面积为16,△CDE的面积为4,AD=7,DE:BE=1:3.
如图所示,已知四边形ABCD的对角线AC、BD相交于点E,△AED∽△BEC,其中A、E、D三点的对应点分别为B、E、C三点,∠ADE=∠ACD,若△ABE的面积为16,△CDE的面积为4,AD=7,DE:BE=1:3. 如图,过正方形ABCD的顶点作对角线BD的平行线,在这条线上取一点E,使BE=BD,连结DE,BE交AD于F,求证:DE2=EF•DB.
如图,过正方形ABCD的顶点作对角线BD的平行线,在这条线上取一点E,使BE=BD,连结DE,BE交AD于F,求证:DE2=EF•DB.