题目内容
9.解下列不等式组,并把它们的解集分别表示在数轴上(1)-$\frac{1}{5}$<1-$\frac{1}{5}$x<$\frac{3}{5}$
(2)$\left\{\begin{array}{l}{\frac{1}{2}+\frac{2}{3}x≤\frac{-x}{2}+\frac{5}{3}}\\{3(x-1)<x-5}\end{array}\right.$.
分析 (1)将原不等式组转化为一元一次不等式组的一般形式,再分别求出每一个不等式的解集,根据口诀:大小小大中间找确定不等式组的解集,表示在数轴上即可;
(2)分别求出每一个不等式的解集,根据口诀:同小取小确定不等式组的解集后,将解集表示在数轴上即可.
解答 解:(1)原不等式组可化为:$\left\{\begin{array}{l}{1-\frac{1}{5}x<\frac{3}{5}}&{①}\\{1-\frac{1}{5}x>-\frac{1}{5}}&{②}\end{array}\right.$,
解不等式①得:x>2,
解不等式②得:x<6,
∴原不等式组的解集为:2<x<6,
解集表示在数轴上如图:
(2)$\left\{\begin{array}{l}{\frac{1}{2}+\frac{2}{3}x≤\frac{-x}{2}+\frac{5}{3}}&{①}\\{3(x-1)<x-5}&{②}\end{array}\right.$,
解不等式①得:x≤1,
解不等式②得:x<-1,
∴不等式组的解集为:x<-1,
解集表示在数轴上如图:
点评 本题考查了一元一次不等式组的解法:解一元一次不等式组时,一般先求出其中各不等式的解集,再求出这些解集的公共部分,解集的规律:同大取大;同小取小;大小小大中间找;大大小小找不到.

练习册系列答案
相关题目
19.在下列图形中,既是轴对称图形,又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
1.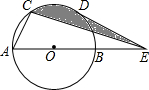 如图所示,在半径为2cm的⊙O中,点C、点D是弧AB的三等分点,点E是直径AB的延长线上一点,连结CE、DE,则图中阴影部分的面积是( )
如图所示,在半径为2cm的⊙O中,点C、点D是弧AB的三等分点,点E是直径AB的延长线上一点,连结CE、DE,则图中阴影部分的面积是( )
 如图所示,在半径为2cm的⊙O中,点C、点D是弧AB的三等分点,点E是直径AB的延长线上一点,连结CE、DE,则图中阴影部分的面积是( )
如图所示,在半径为2cm的⊙O中,点C、点D是弧AB的三等分点,点E是直径AB的延长线上一点,连结CE、DE,则图中阴影部分的面积是( )| A. | $\sqrt{3}$ | B. | $\frac{2π}{3}$ | C. | $\frac{2π}{3}-\sqrt{3}$ | D. | $\frac{2π}{3}$+$\sqrt{3}$ |
18.一组数据:3,4,5,6,6,的平均数、众数、中位数分别是( )
| A. | 4.8,6,6 | B. | 5,5,5 | C. | 4.8,6,5 | D. | 5,6,6 |
19.在-$\frac{1}{3}$,$\frac{1}{2013}$,-1,0这四个数中最小的是( )
| A. | -$\frac{1}{3}$ | B. | $\frac{1}{2013}$ | C. | -1 | D. | 0 |
 如图,A(2,1),B(1,-1),以O为位似中心,按比例尺1:2,把△AOB放大,则点A的对应点A′的坐标为(4,2)或(-4,-2).
如图,A(2,1),B(1,-1),以O为位似中心,按比例尺1:2,把△AOB放大,则点A的对应点A′的坐标为(4,2)或(-4,-2).

 若抛物线y=ax2+bx+c如图所示,下列四个结论:
若抛物线y=ax2+bx+c如图所示,下列四个结论: