题目内容
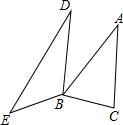 如图,在△ABC和△BDE中,∠ABC+∠DBE=180°,且BA=BD,BC=BE.设△ABC的面积为S1,△BDE的面积为S2,则S1,S2具有的数量关系是
如图,在△ABC和△BDE中,∠ABC+∠DBE=180°,且BA=BD,BC=BE.设△ABC的面积为S1,△BDE的面积为S2,则S1,S2具有的数量关系是考点:三角形的面积
专题:
分析:如图,作辅助线;证明AM=DF,此为解决该题的关键性结论;借助面积公式即可解决问题.
解答: 解:如图,过点D作DF⊥EB,AM⊥BC;
解:如图,过点D作DF⊥EB,AM⊥BC;
设∠ABC=α,∠DBE=β;
∵∠ABC+∠DBE=180°,
∴α=180°-β,
∴sinα=sin(180°-β)=sinβ;
∵sinα=
,sin∠DBF=sinβ=
,
∴
=
;而AB=BD,
∴AM=DF;而BE=BC,
∴S1=S2,
故答案为:相等.
 解:如图,过点D作DF⊥EB,AM⊥BC;
解:如图,过点D作DF⊥EB,AM⊥BC;设∠ABC=α,∠DBE=β;
∵∠ABC+∠DBE=180°,
∴α=180°-β,
∴sinα=sin(180°-β)=sinβ;
∵sinα=
| AM |
| AB |
| DF |
| BD |
∴
| AM |
| AB |
| DF |
| BD |
∴AM=DF;而BE=BC,
∴S1=S2,
故答案为:相等.
点评:该题主要考查了三角形中的边角关系、三角形的面积公式及其应用问题;解题的关键是作辅助线,借助三角形的边角关系来分析、判断.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案
相关题目
在Rt△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于点E,AC=5,AB=8,则BE=( )
| A、3 | B、4 | C、5 | D、6 |
 如图,两个边长分别为4cm与3cm的正方形的一部分重叠在一起,重叠部分是边长为acm的正方形,则图中阴影部分的面积总和是
如图,两个边长分别为4cm与3cm的正方形的一部分重叠在一起,重叠部分是边长为acm的正方形,则图中阴影部分的面积总和是