题目内容
在Rt△ABC中,∠C=90°,若此三角形的周长是30,c=13,则此三角形的面积是 .
考点:勾股定理
专题:计算题
分析:设BC=a=x,根据周长与c的值,表示出AC,即为b,利用勾股定理求出x的值,确定出a与b,即可求出三角形的面积.
解答:解:在Rt△ABC中,∠C=90°,且三角形的周长是30,c=13,
设BC=a=x,可得AC=b=30-13-x=17-x,
根据勾股定理得:x2+(17-x)2=132,即x2-17x+60=0,
分解因式得:(x-5)(x-12)=0,
解得:x=5或x=12,
∴a=5,b=12;a=12,b=5,
则S△ABC=
ab=30.
故答案为:30.
设BC=a=x,可得AC=b=30-13-x=17-x,
根据勾股定理得:x2+(17-x)2=132,即x2-17x+60=0,
分解因式得:(x-5)(x-12)=0,
解得:x=5或x=12,
∴a=5,b=12;a=12,b=5,
则S△ABC=
| 1 |
| 2 |
故答案为:30.
点评:此题考查了勾股定理,熟练掌握勾股定理是解本题的关键.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目
若最简二次根式
和
是同类二次根式,则a的值是( )
| 2a-4 |
| 2 |
| A、a=2 | B、a=-2 |
| C、a=3 | D、a=-3 |
 已知,如图∠ABD=∠EBC,∠BAD=∠BCE,求证:△DEB∽△ABC.
已知,如图∠ABD=∠EBC,∠BAD=∠BCE,求证:△DEB∽△ABC.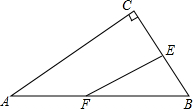 如图,在△ABC中,AC⊥BC,AB=10cm,BC=6cm,F点以2cm/秒的速度在线段AB上由A向B匀速运动,E点同时以1cm/秒的速度在线段BC上由B向C匀速运动,设运动时间为t秒(0<t<5).
如图,在△ABC中,AC⊥BC,AB=10cm,BC=6cm,F点以2cm/秒的速度在线段AB上由A向B匀速运动,E点同时以1cm/秒的速度在线段BC上由B向C匀速运动,设运动时间为t秒(0<t<5).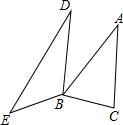 如图,在△ABC和△BDE中,∠ABC+∠DBE=180°,且BA=BD,BC=BE.设△ABC的面积为S1,△BDE的面积为S2,则S1,S2具有的数量关系是
如图,在△ABC和△BDE中,∠ABC+∠DBE=180°,且BA=BD,BC=BE.设△ABC的面积为S1,△BDE的面积为S2,则S1,S2具有的数量关系是 如图所示,用三种大小不同的六个正方形和一个缺角的正方形拼成长方形ABCD,其中,GH=2cm,GK=2cm,设BF=xcm,
如图所示,用三种大小不同的六个正方形和一个缺角的正方形拼成长方形ABCD,其中,GH=2cm,GK=2cm,设BF=xcm,