Question

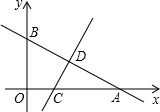如图，一次函数y=kx+b的图象与坐标轴分别交于点A（8，0）和B（0，6），再将△AOB沿直线CD折起，使点A与点B重合，直线CD与x轴交于点C，与AB交于点D．
（1）试确定直线AB的函数解析式；
（2）求点C的坐标．
（3）是否存在经过点E（2，0）的直线l将△OBA的面积分成1：3？如果存在求出直线的解析式，不存在试说明理由．

Answer 1

考点：一次函数综合题

专题：综合题

分析：（1）将A与B坐标代入一次函数解析式求出k与b的值，即可确定出直线AB解析式；
（2）连接BC，由折叠的性质得到BC=AC，在直角三角形BOC中，设BC=AC=x，表示出OC=8-x，由OB=6，利用勾股定理列出关于x的方程，求出方程的解得到x的值，确定出OC的长，即可得出C坐标；
（3）存在，做出直线EF，与直线AB交于点F，作FG⊥x轴，根据题意得：S_△AEF=

3

4

S_△ABC或S_△AEF=

1

4

S_△ABC，求出FG长，联立直线EF与AB，消去y表示出x，进而表示出y，根据纵坐标为EF列出关于a的方程，求出方程的解得到a的值，即可确定出满足题意的直线解析式．

解答：解：（1）将A（8，0）与B（0，6）代入一次函数解析式得：

8k+b=0 b=6

，
解得：

k=- 3 4 b=6

，
则直线AB解析式为y=-

3

4

x+6；

（2）连接BC，由折叠得到AC=BC，
∵A（8，0），B（0，6），
∴OA=8，OB=6，
在Rt△BOC中，设CB=CA=x，则有OC=OA-AC=8-x，
根据勾股定理得：BC²=OB²+OC²，即x²=（8-x）²+6²，
解得：x=

25

4

，
∴OC=8-x=

7

4

，即C（

7

4

，0）；

（3）存在，做出直线EF，与直线AB交于点F，作FG⊥x轴，
根据题意得：S_△AEF=

3

4

S_△ABC或S_△AEF=

1

4

S_△ABC，
即

1

2

AE•FG=

3

4

×

1

2

OA•OB或

1

2

AE•FG=

1

4

×

1

2

OA•OB，
由AE=OA-OE=8-2=6，OA=8，OB=6，
解得：FG=6或FG=2，
理由为：设过E的直线方程为y=a（x-2）=ax-2a，
与直线AB解析式联立消去y得：ax-2a=-

3

4

x+6，
解得：x=

8a+24

4a+3

，
∴y=a（

8a+24

4a+3

-2）=6或2，
解得：a=-3或a=

3

5

，
则满足题意的直线方程为y=-3x+6或y=

3

5

x-

6

5

．

点评：此题属于一次函数综合题，涉及的知识有：待定系数法求一次函数解析式，坐标与图形性质，勾股定理，利用了方程的思想，熟练掌握待定系数法是解本题的关键．