题目内容
在Rt△ABC中，∠C=90°，若sinA=
，求cosA，sinB，cosB．
| 12 |
| 13 |
考点：互余两角三角函数的关系,同角三角函数的关系
专题：
分析：先根据sin2α+cos2α=1计算出cosA=
，然后根据互余两角三角函数的关系求解．
| 5 |
| 13 |
解答：解：∵∠C=90°，sinA=
，
∴cosA=
=
，
∵∠A+∠B=90°，
∴sinB=cosA=
，cosB=sinA=
．
| 12 |
| 13 |
∴cosA=
1-(
|
| 5 |
| 13 |
∵∠A+∠B=90°，
∴sinB=cosA=
| 5 |
| 13 |
| 12 |
| 13 |
点评：本题考查了互余两角三角函数的关系：在直角三角形中，∠A+∠B=90°时，sinA=cosB或sinB=cosA．也考查了同角三角形函数的关系．
练习册系列答案
相关题目
在代数式
、
、
、
中，是分式的有（ ）
| 1 |
| x |
| xy-y |
| 3xy |
| a+b |
| 5 |
| x+y |
| π |
| A、1个 | B、2个 | C、3个 | D、4个 |
下列各式：①
，②
，③
，④
，其中是分式的有（ ）
| 1 |
| a |
| x |
| 1+π |
| x-1 |
| 5 |
| 2 |
| 2x+y |
| A、①②③④ | B、①④ |
| C、①②④ | D、②④ |
如图，在△ABC中，AB=AC，∠BAC=120°，AB的垂直平分线交AB于点E，交BC于点F，连接AF，求∠AFC的度数．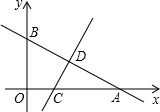
如图，一次函数y=kx+b的图象与坐标轴分别交于点A（8，0）和B（0，6），再将△AOB沿直线CD折起，使点A与点B重合，直线CD与x轴交于点C，与AB交于点D．
已知，如图，AB∥CD，∠ABE=3∠ABF，∠CDE=3∠CDF，试求∠E与∠F的比．