题目内容
 如图是两个直径为30cm和一个直径为50cm的水泥涵管堆放的截面图,下面两个较细的涵管被两排相距78cm的桩堵住,求涵管堆放的高度.(不计木桩的直径).
如图是两个直径为30cm和一个直径为50cm的水泥涵管堆放的截面图,下面两个较细的涵管被两排相距78cm的桩堵住,求涵管堆放的高度.(不计木桩的直径).考点:相切两圆的性质
专题:
分析:首先连接AB,BC,AC,过点A作AD⊥BC于点D,易求得AB=AC=40cm,BC=48cm,然后利用等腰三角形的性质与勾股定理,求得AD的长,继而求得答案.
解答: 解:如图,连接AB,BC,AC,过点A作AD⊥BC于点D,
解:如图,连接AB,BC,AC,过点A作AD⊥BC于点D,
∵水泥涵管的直径为30cm和50cm;
∴半径为:15cm,25cm,
根据题意得:AB=AC=15+25=40(cm),BC=78-30=48(cm),
∴BD=CD=
BC=
×48=24(cm),
∴AD=
=32(cm),
∴涵管堆放的高度为:32+15+25=72(cm).
答:涵管堆放的高度为72cm.
 解:如图,连接AB,BC,AC,过点A作AD⊥BC于点D,
解:如图,连接AB,BC,AC,过点A作AD⊥BC于点D,∵水泥涵管的直径为30cm和50cm;
∴半径为:15cm,25cm,
根据题意得:AB=AC=15+25=40(cm),BC=78-30=48(cm),
∴BD=CD=
| 1 |
| 2 |
| 1 |
| 2 |
∴AD=
| AB2-BD2 |
∴涵管堆放的高度为:32+15+25=72(cm).
答:涵管堆放的高度为72cm.
点评:此题考查了相切两圆的性质、等腰三角形的性质以及勾股定理.此题难度适中,注意掌握辅助线的作法,注意掌握数形结合思想的应用.

练习册系列答案
相关题目
下列各式:①
,②
,③
,④
,其中是分式的有( )
| 1 |
| a |
| x |
| 1+π |
| x-1 |
| 5 |
| 2 |
| 2x+y |
| A、①②③④ | B、①④ |
| C、①②④ | D、②④ |
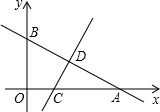 如图,一次函数y=kx+b的图象与坐标轴分别交于点A(8,0)和B(0,6),再将△AOB沿直线CD折起,使点A与点B重合,直线CD与x轴交于点C,与AB交于点D.
如图,一次函数y=kx+b的图象与坐标轴分别交于点A(8,0)和B(0,6),再将△AOB沿直线CD折起,使点A与点B重合,直线CD与x轴交于点C,与AB交于点D. 已知:在△ABC中,AB=AC,AD是外角∠CAE的平分线.求证:AD∥BC.
已知:在△ABC中,AB=AC,AD是外角∠CAE的平分线.求证:AD∥BC. 已知,如图,AB∥CD,∠ABE=3∠ABF,∠CDE=3∠CDF,试求∠E与∠F的比.
已知,如图,AB∥CD,∠ABE=3∠ABF,∠CDE=3∠CDF,试求∠E与∠F的比.