题目内容
14. A(0,4)是直角坐标系y轴上一点,P是x轴上一动点,从原点O出发,沿正半轴运动,速度为每秒1个单位长度,以P为直角顶点在第一象限内作等腰Rt△APB.设P点的运动时间为t秒.
A(0,4)是直角坐标系y轴上一点,P是x轴上一动点,从原点O出发,沿正半轴运动,速度为每秒1个单位长度,以P为直角顶点在第一象限内作等腰Rt△APB.设P点的运动时间为t秒.(1)若AB∥x轴,求t的值;
(2)设点B的坐标为(x,y),试求y关于x的函数表达式;
(3)当t=3时,平面直角坐标系内有一点M(3,a),请直接写出使△APM为等腰三角形的点M的坐标.
分析 (1)由AB∥x轴,可找出四边形ABCO为长方形,再根据△APB为等腰三角形可得知∠OAP=45°,从而得出△AOP为等腰直角三角形,由此得出结论;
(2)先证出△PAO≌△BPC,即可得出各边的关系,利用坐标系中点的意义即可得出个线段的长度,由相等的量可得出结论;
(3)由等腰三角形的性质可知,若△APM为等腰三角形只需找到一组临边相等即可,临边相等分三种情况,分类讨论结合两点间的距离公式即可得出结论.
解答 解:(1)过点B作BC⊥x轴于点C,如图1所示.
∵AO⊥x轴,BC⊥x轴,且AB∥x轴,
∴四边形ABCO为长方形,
∴AO=BC=4.
∵△APB为等腰直角三角形,
∴AP=BP,∠PAB=∠PBA=45°,
∴∠OAP=90°-∠PAB=45°,
∴△AOP为等腰直角三角形,
∴OA=OP=4.
t=4÷1=4(秒),
故t的值为4.
(2)∵△APB为等腰直角三角形,
∴∠APO+∠BPC=180°-90°=90°.
又∵∠PAO+∠APO=90°,
∴∠PAO=∠BPC.
在△PAO和△BPC中,$\left\{\begin{array}{l}{∠PAO=∠BPC}\\{∠AOP=∠PCB=90°}\\{AP=BP}\end{array}\right.$,
∴△PAO≌△BPC,
∴AO=PC,BC=PO.
∵点A(0,4),点P(t,0),点B(x,y),
∴PC=AO=4,BC=PO=t=y,CO=PC+PO=4+y=x,
∴y=x-4.
(3)△APM为等腰三角形分三种情况:
①当AM=AP时,如图2所示.
当t=3时,点P(3,0),
∵点M(3,a),点A(0,4),
∴由两点间的距离公式可知:
AM=$\sqrt{(3-0)^{2}+(a-4)^{2}}$,AP=$\sqrt{(3-0)^{2}+(0-4)^{2}}$=5,
∴$\sqrt{(3-0)^{2}+(a-4)^{2}}$=5,解得:a=0(舍去),a=8.
此时M点的坐标为(3,8);
②当MA=MP时,如图3所示.
∵点P(3,0),点A(0,4),点M(3,a),
∴由两点间的距离公式可知:
MA=$\sqrt{(3-0)^{2}+(a-4)^{2}}$,MP=a,
∴$\sqrt{(3-0)^{2}+(a-4)^{2}}$=a,解得:a=$\frac{25}{8}$.
此时M点的坐标为(3,$\frac{25}{8}$);
③当PA=PM时,如图4所示.
∵点P(3,0),点A(0,4),点M(3,a),
∴由两点间的距离公式可知:
PA=$\sqrt{(3-0)^{2}+(0-4)^{2}}$=5,PM=|a|,
∴a=±5.
此时M点的坐标为(3,5)或(3,-5).
综上可知:当t=3时,平面直角坐标系内有一点M(3,a),使△APM为等腰三角形的点M的坐标为(3,8),(3,$\frac{25}{8}$),(3,5)和(3,-5).
点评 本题考查了长方形的判定及性质、全等三角形的判定及性质、等腰三角形的性质和两点间的距离公式,解题的关键是:(1)找出△AOP为等腰直角三角形;(2)利用△PAO≌△BPC找出相等的边;(3)利用两点间的距离公式表示出两线段的长度.本题属于中档题,难度不大,(1)(3)问容易解决,(2)需要用x、t、y去表示各边长度,再由相等的边找到x、y的关系,作此类型的题要结合图形,寻找相等的量才能得出结论.

 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案 在如图所示的花坛的图案中,圆形的内部有菊花组成的内接等边三角形,则这个图案( )
在如图所示的花坛的图案中,圆形的内部有菊花组成的内接等边三角形,则这个图案( )| A. | 是轴对称图形但不是中心对称图形 | |
| B. | 既是轴对称图形又是中心对称图形 | |
| C. | 是中心对称图形但不是轴对称图形 | |
| D. | 既不是轴对称图形又不是中心对称图形 |
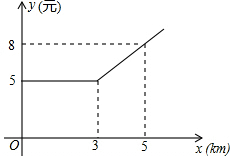 某县出租车计费方法如图所示,x(km)表示行驶里程,y(元)表示车费,请根据图象回答下列问题.
某县出租车计费方法如图所示,x(km)表示行驶里程,y(元)表示车费,请根据图象回答下列问题.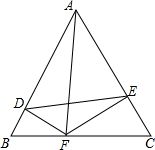 已知△ABC为等边三角形,F为BC上一点,FD⊥AB于D,FE⊥AC于E.求证:$\frac{BF}{CF}=\frac{BD}{CE}$.
已知△ABC为等边三角形,F为BC上一点,FD⊥AB于D,FE⊥AC于E.求证:$\frac{BF}{CF}=\frac{BD}{CE}$.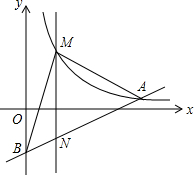 如图,在平面直角坐标系中,已知点A(8,1),B(0,-3),反比例函数y=$\frac{k}{x}$(a>0)的图象经过点A,动直线x=t,(0<t<8)与反比例函数的图象交于点M,与直线AB交于点N.
如图,在平面直角坐标系中,已知点A(8,1),B(0,-3),反比例函数y=$\frac{k}{x}$(a>0)的图象经过点A,动直线x=t,(0<t<8)与反比例函数的图象交于点M,与直线AB交于点N.