题目内容
7.在△ABC中,AB=AC=5,BC=6,AD平分∠BAC交BC于点D,则BC边上的高线长是( )| A. | 3 | B. | 3.6 | C. | 4 | D. | 4.8 |
分析 首先根据等腰三角形的性质:等腰三角形的三线合一,求出DB=DC=$\frac{1}{2}$CB,AD⊥BC,再利用勾股定理求出AD的长即可.
解答 解:∵AB=AC,AD是∠BAC的角平分线,
∴DB=DC=$\frac{1}{2}$CB=3,AD⊥BC,
在Rt△ABD中,
∵AD2+BD2=AB2,
∴AD=$\sqrt{A{B}^{2}-B{D}^{2}}$=4,
故选C.
点评 此题主要考查了等腰三角形的性质与勾股定理的应用,做题的关键是根据等腰三角形的性质证出△ADB是直角三角形.

练习册系列答案
相关题目
15.某种蔬菜按品质分成三个等级销售,销售情况如表:
则售出蔬菜的平均单价为44元/千克.
| 等级 | 单价(元/千克) | 销售量(千克) |
| 一等 | 50 | 20 |
| 二等 | 45 | 40 |
| 三等 | 40 | 40 |
19. 在如图所示的花坛的图案中,圆形的内部有菊花组成的内接等边三角形,则这个图案( )
在如图所示的花坛的图案中,圆形的内部有菊花组成的内接等边三角形,则这个图案( )
 在如图所示的花坛的图案中,圆形的内部有菊花组成的内接等边三角形,则这个图案( )
在如图所示的花坛的图案中,圆形的内部有菊花组成的内接等边三角形,则这个图案( )| A. | 是轴对称图形但不是中心对称图形 | |
| B. | 既是轴对称图形又是中心对称图形 | |
| C. | 是中心对称图形但不是轴对称图形 | |
| D. | 既不是轴对称图形又不是中心对称图形 |
16.一个不透明的袋中装有大小相同的2个红球和2个绿球,如果先从袋中摸出1个球后不放回,再摸出1个球,则两次摸到的球中有个绿球和1个红球的概率是( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{5}{6}$ |
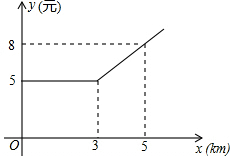 某县出租车计费方法如图所示,x(km)表示行驶里程,y(元)表示车费,请根据图象回答下列问题.
某县出租车计费方法如图所示,x(km)表示行驶里程,y(元)表示车费,请根据图象回答下列问题.