题目内容
 在△ABC中,∠ACB=90°,CD是高.CA:CB=m:n,求证:AD:DB=m2:n2.
在△ABC中,∠ACB=90°,CD是高.CA:CB=m:n,求证:AD:DB=m2:n2.考点:相似三角形的判定与性质
专题:证明题
分析:易证△ABC∽△ACD,△ABC∽△CBD,根据全等三角形对应边比例相等的性质即可解题.
解答:证明:∵∠A+∠ACD=90°,∠B+∠BCD=90°,∠ACD+∠BCD=90°,
∴∠A=∠BCD,∠B=∠ACD,
∴△ABC∽△ACD,△ABC∽△CBD,
∴
=
=
=
,
∴
=
.
∴∠A=∠BCD,∠B=∠ACD,
∴△ABC∽△ACD,△ABC∽△CBD,
∴
| CA |
| CB |
| AD |
| CD |
| CD |
| BD |
| m |
| n |
∴
| AD |
| BD |
| m2 |
| n2 |
点评:本题考查了相似三角形的判定,考查了相似三角形对应边比例相等的性质.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
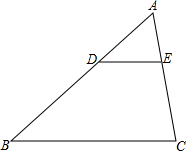 如图,在△ABC中,点D是AB边上一点,DE∥BC交AC于E,AD:DB=1:2,则△ADE与△ABC的面积之比为( )
如图,在△ABC中,点D是AB边上一点,DE∥BC交AC于E,AD:DB=1:2,则△ADE与△ABC的面积之比为( )| A、1:2 | B、1:4 |
| C、1:8 | D、1:9 |
无论m取何实数,直线y=x+3m与y=-x+1的交点不可能在( )
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
 如图,正五边形ABCDE内接于⊙O,求∠ABD的度数.
如图,正五边形ABCDE内接于⊙O,求∠ABD的度数.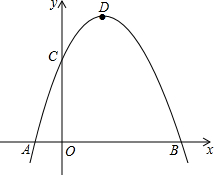 如图,抛物线y=-x2+2x+3与x轴相交于A,B两点(点A在点B的左侧),与y轴相交于点C,顶点为D.
如图,抛物线y=-x2+2x+3与x轴相交于A,B两点(点A在点B的左侧),与y轴相交于点C,顶点为D.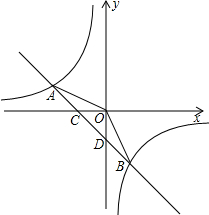 如图,反比例函数y=
如图,反比例函数y=