题目内容
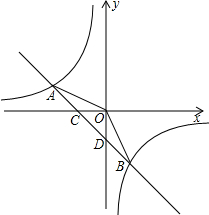 如图,反比例函数y=
如图,反比例函数y=| k |
| x |
(1)求反比例函数y=
| k |
| x |
(2)求△AOB的面积.
考点:反比例函数与一次函数的交点问题
专题:
分析:(1)将A坐标代入反比例解析式求出k的值,确定出反比例解析式,将B坐标代入反比例解析式求出m的值,确定出B坐标,将A与B坐标代入一次函数解析式求出a与b的值,即可确定出一次函数解析式;
(2)由一次函数解析式求出C坐标,确定出OC长,三角形AOB面积=三角形AOC面积+三角形BOC面积,求出即可.
(2)由一次函数解析式求出C坐标,确定出OC长,三角形AOB面积=三角形AOC面积+三角形BOC面积,求出即可.
解答:解:(1)将A(-4,2)代入反比例y=
得:k=-8,
∴反比例解析式为y=-
;
将B(m,-4)代入反比例解析式得:m=2,即B(2,-4),
将A与B代入一次函数解析式得:
,
解得:
.
∴一次函数解析式为y=-x-2;
(2)由y=-x-2;
令y=0,得到x=-2,即OC=2,
∴S△AOB=S△AOC+S△BOC=
×2×2+
×2×4=6.
| k |
| x |
∴反比例解析式为y=-
| 8 |
| x |
将B(m,-4)代入反比例解析式得:m=2,即B(2,-4),
将A与B代入一次函数解析式得:
|
解得:
|
∴一次函数解析式为y=-x-2;
(2)由y=-x-2;
令y=0,得到x=-2,即OC=2,
∴S△AOB=S△AOC+S△BOC=
| 1 |
| 2 |
| 1 |
| 2 |
点评:此题考查了一次函数与反比例函数的交点问题,利用了待定系数法及数形结合的思想,熟练掌握待定系数法是解本题的关键.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
 如图,A,B,C三点在⊙O上,且∠AOB=70°,则∠ACB等于( )
如图,A,B,C三点在⊙O上,且∠AOB=70°,则∠ACB等于( )| A、110° | B、70° |
| C、55° | D、35° |
 在△ABC中,∠ACB=90°,CD是高.CA:CB=m:n,求证:AD:DB=m2:n2.
在△ABC中,∠ACB=90°,CD是高.CA:CB=m:n,求证:AD:DB=m2:n2.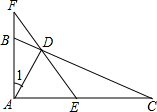 如图,已知在△ABC中,∠BAC=90°,AD⊥BC,E是AC的中点,ED交AB的延长线与F,
如图,已知在△ABC中,∠BAC=90°,AD⊥BC,E是AC的中点,ED交AB的延长线与F,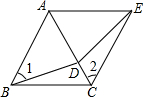 已知:如图所示,D在等边△ABC的边AC上,∠ACE=∠ABD,CE=BD.试说明:
已知:如图所示,D在等边△ABC的边AC上,∠ACE=∠ABD,CE=BD.试说明: 如图,数轴上点A表示2,点B表示
如图,数轴上点A表示2,点B表示