题目内容
 如图所示,直线l1与两坐标轴的交点坐标分别是A(-3,0),B(0,4),O是坐标系原点.
如图所示,直线l1与两坐标轴的交点坐标分别是A(-3,0),B(0,4),O是坐标系原点.(1)求直线l1的函数表达式;
(2)若将AO沿直线AC折叠,使点O落在斜边AB上,且与AD重合;
①求点C标;
②求直线AC、直线l1和y轴所围图形的面积.
考点:一次函数综合题,勾股定理,轴对称的性质
专题:综合题
分析:(1)只需运用待定系数法就可解决问题;
(2)①可设OC=x,由折叠可得AD=AO=3,CD=CO,∠ADC=∠AOC=90°.然后在Rt△BDC中运用勾股定理建立方程,解方程就可得到点C的坐标;②由于直线AC、直线l1和y轴所围图形就是△ABC,只需求出该三角形的面积即可.
(2)①可设OC=x,由折叠可得AD=AO=3,CD=CO,∠ADC=∠AOC=90°.然后在Rt△BDC中运用勾股定理建立方程,解方程就可得到点C的坐标;②由于直线AC、直线l1和y轴所围图形就是△ABC,只需求出该三角形的面积即可.
解答:解:(1)设直线l1的函数表达式为y=kx+b,
∵A(-3,0)、B(0,4)在直线l1上,
∴
,
∴
,
∴直线l1的函数表达式为y=
x+4;
(2)①∵A(-3,0),B(0,4),∴OA=3,OB=4.
∵∠AOB=90°,∴AB=5.
由折叠可得:AD=AO=3,CD=CO,∠ADC=∠AOC=90°.
设OC=x,则CD=x,BC=4-x.
∵∠ADC=90°,∴∠BDC=90°.
在Rt△BDC中,
∵BD=AB-AD=5-3=2,CD=x,BC=4-x,
∴22+x2=(4-x)2,
解得:x=
,
∴点C的坐标为(0,
);
②由图可知:直线AC、直线l1和y轴所围图形是△ABC,
S△ABC=
BC•OA=
×(4-
)×3=
,
∴直线AC、直线l1和y轴所围图形的面积为
.
∵A(-3,0)、B(0,4)在直线l1上,
∴
|
∴
|
∴直线l1的函数表达式为y=
| 4 |
| 3 |
(2)①∵A(-3,0),B(0,4),∴OA=3,OB=4.

∵∠AOB=90°,∴AB=5.
由折叠可得:AD=AO=3,CD=CO,∠ADC=∠AOC=90°.
设OC=x,则CD=x,BC=4-x.
∵∠ADC=90°,∴∠BDC=90°.
在Rt△BDC中,
∵BD=AB-AD=5-3=2,CD=x,BC=4-x,
∴22+x2=(4-x)2,
解得:x=
| 3 |
| 2 |
∴点C的坐标为(0,
| 3 |
| 2 |
②由图可知:直线AC、直线l1和y轴所围图形是△ABC,
S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 15 |
| 4 |
∴直线AC、直线l1和y轴所围图形的面积为
| 15 |
| 4 |
点评:本题主要考查了用待定系数法求一次函数的解析式、勾股定理、轴对称的性质、解一元一次方程等知识,运用勾股定理建立方程是解决第(2)小题的关键.

练习册系列答案
相关题目
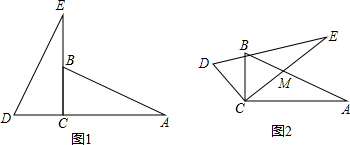
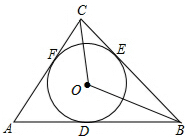 如图,圆O与△ABC的三边分别相切于点D,E,F,连接OB,OC,求证:∠BOC=90°-
如图,圆O与△ABC的三边分别相切于点D,E,F,连接OB,OC,求证:∠BOC=90°-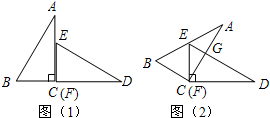 如图,已知△ACB与△DFE是两个全等的直角三角形,量得它们的斜边长为10cm,较小锐角为30°,将这两个三角形摆成如图(1)所示的形状,使点B、C、F、D在同一条直线上,且点C与点F重合,将图(1)中的△ACB绕点C顺时针方向旋转到图(2)的位置,点E在AB边上,AC交DE于点G,则BD之间的距离为
如图,已知△ACB与△DFE是两个全等的直角三角形,量得它们的斜边长为10cm,较小锐角为30°,将这两个三角形摆成如图(1)所示的形状,使点B、C、F、D在同一条直线上,且点C与点F重合,将图(1)中的△ACB绕点C顺时针方向旋转到图(2)的位置,点E在AB边上,AC交DE于点G,则BD之间的距离为 如图,已知:A、F、C、D四点在一条直线上,AF=CD,DE∥AB,且AB=DE.求证:EF∥CB.
如图,已知:A、F、C、D四点在一条直线上,AF=CD,DE∥AB,且AB=DE.求证:EF∥CB.