题目内容
已知一次函数y=kx+b的图象经过一、二、四象限,则直线y=bx-k的图象可能是( )
A、 |
B、 |
C、 |
D、 |
考点:一次函数图象与系数的关系
专题:
分析:根据一次函数y=kx+b图象在坐标平面内的位置关系先确定k,b的取值范围,再根据k,b的取值范围确定一次函数y=bx-k图象在坐标平面内的位置关系,从而求解.
解答:解:一次函数y=kx+b过一、二、四象限,
则函数值y随x的增大而减小,因而k<0;
图象与y轴的正半轴相交则b>0,
因而一次函数y=bx-k的一次项系数b>0,
y随x的增大而增大,经过一三象限,
常数项-k>0,则函数与y轴正半轴相交,
因而一定经过一、二、三象限,
故选B.
则函数值y随x的增大而减小,因而k<0;
图象与y轴的正半轴相交则b>0,
因而一次函数y=bx-k的一次项系数b>0,
y随x的增大而增大,经过一三象限,
常数项-k>0,则函数与y轴正半轴相交,
因而一定经过一、二、三象限,
故选B.
点评:本题考查了一次函数的图象与系数的关系.函数值y随x的增大而减小?k<0;函数值y随x的增大而增大?k>0;
一次函数y=kx+b图象与y轴的正半轴相交?b>0,一次函数y=kx+b图象与y轴的负半轴相交?b<0,一次函数y=kx+b图象过原点?b=0.
一次函数y=kx+b图象与y轴的正半轴相交?b>0,一次函数y=kx+b图象与y轴的负半轴相交?b<0,一次函数y=kx+b图象过原点?b=0.

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
下列条件中能组成三角形的是( )
| A、7cm,7cm,12cm |
| B、5cm,3cm,9cm |
| C、6cm,9cm,16cm |
| D、5cm,6cm,11cm |
有4条线段长度分别为2cm,3cm,4cm,5cm,从中任意取三条线段能组成三角形的概率是( )
A、
| ||
B、
| ||
C、
| ||
| D、1 |
对于反比例函数y=
(k<0),下列说法正确的是( )
| k |
| x |
| A、图象经过点(1,-k) |
| B、图象位于第一、三象限 |
| C、图象是中心对称图形 |
| D、当x<0时,y随x的增大而减小 |
对角线互相垂直平分的四边形是( )
| A、菱形 | B、矩形 |
| C、平行四边形 | D、任意四边形 |
下列方程中,一元二次方程共( )
①3x2+x=20;②x2+y2=5;③x2-
=4;④x2=1;⑤x2-
+3=0.
①3x2+x=20;②x2+y2=5;③x2-
| 1 |
| x |
| x |
| 3 |
| A、5个 | B、4个 | C、3个 | D、2个 |
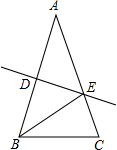 如图,在△ABC中,AB=AC,AB的垂直平分线交AC于点E,垂足为点D,连接BE,如图AB=10,BC=3,则△EBC的周长为( )
如图,在△ABC中,AB=AC,AB的垂直平分线交AC于点E,垂足为点D,连接BE,如图AB=10,BC=3,则△EBC的周长为( )| A、10 | B、13 | C、16 | D、23 |
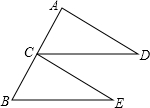 如图,C是线段AB的中点,CD∥BE,且CD=BE,求证:AD=CE.
如图,C是线段AB的中点,CD∥BE,且CD=BE,求证:AD=CE.