题目内容
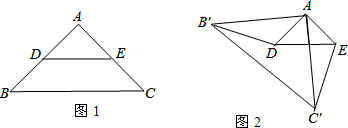
20.在△ABC中,AB=AC,∠BAC=90°,D、E分别是AB、AC边的中点.将△ABC绕点A顺时针旋转α角(0°<α<180°),得到△AB′C′(如图2).(1)探究DB′与EC′的数量关系,并给予证明;
(2)当DB′∥AE时,在图1中用尺规作出旋转后的图形,直接写出旋转角α的度数60°.
分析 (1)根据旋转的性质得到AB′=AB=AC′=AC,∠B′AC′=∠BAC=90°,则利用等角的余角相等得∠DAB′=∠EAC′,然后利用“SAS”证明△ADB′≌△AEC′,所以DB′=EC′;
(2)过D点作AB的垂线,再以点A为圆心,AB为半径画弧交垂线于B′,接着过A点作AC′⊥AB′,且AC′=AC,则△AB′C′为所作;由于在Rt△ADB′中,AB′=2AD,所以∠AB′D=30°,则∠DAB′=60°,即旋转角为60°.
解答 解:(1)DB′与EC′相等.利用如下:
如图2,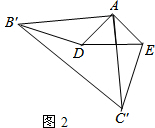
∵AB=AC,D、E分别是AB、AC边的中点,
∴AD=AE,
∵△ABC绕点A顺时针旋转α角(0°<α<180°),得到△AB′C′,
∴AB′=AB=AC′=AC,∠B′AC′=∠BAC=90°,
∴∠DAB′=∠EAC′,
在△ADB′和△AEC′中,
$\left\{\begin{array}{l}{AD=AE}\\{∠DAB′=∠EAC′}\\{AB′=AC′}\end{array}\right.$,
∴△ADB′≌△AEC′,
∴DB′=EC′;
(2)如图1,△AB′C′为所作,
旋转角α的度数为60°.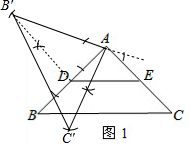
故答案为60°.
点评 本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了作图-旋转变换.

练习册系列答案
相关题目
5.两个连续偶数之积为168,则这两个连续偶数之和为( )
| A. | 26 | B. | -26 | C. | ±26 | D. | 都不对 |
10.下列图形中,不是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
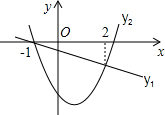 已知函数y1=px+q和y2=ax2+bx+c的图象如图所示,看图回答:
已知函数y1=px+q和y2=ax2+bx+c的图象如图所示,看图回答: