题目内容
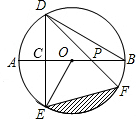 如图,AB是⊙O的直径,弦DE垂直平分半径OA,C为垂足,弦DF与半径OB相交于点P,连接EF、EO.若DE=2
如图,AB是⊙O的直径,弦DE垂直平分半径OA,C为垂足,弦DF与半径OB相交于点P,连接EF、EO.若DE=2| 3 |
(1)求⊙O的半径;
(2)求图中阴影部分及△PBF的面积.
考点:垂径定理,勾股定理,扇形面积的计算
专题:计算题
分析:(1)根据垂径定理由OC⊥DE得EC=
DE=
,由弦DE垂直平分半径OA得OC=
OA=
OE,根据含30度的直角三角形三边的关系得到∠E=30°,OC=
CE=1,所以OE=2;
(2)连结OF,BF,BE,作BH⊥DF于H,如图,根据圆周角定理得∠EOF=2∠EPF=90°,则根据扇形面积公式和图中阴影部分的面积=S扇形EOF-S△OEF计算得到S阴影=π-2;再利用勾股定理计算出BD=2
,易得△BED为等边三角形,则∠BED=60°,所以∠BFD=∠BED=60°,利用△PCD为等腰直角三角形得到PC=DC=
,可计算得PB=3-
,在Rt△PBH中,根据等腰直角三角形的性质可计算出BH=PH=
PB=
,在Rt△BHF中,根据含30度的直角三角形三边的关系得到HF=
BH=
,则PF=PH+HF
,然后根据三角形面积公式计算.
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 3 |
(2)连结OF,BF,BE,作BH⊥DF于H,如图,根据圆周角定理得∠EOF=2∠EPF=90°,则根据扇形面积公式和图中阴影部分的面积=S扇形EOF-S△OEF计算得到S阴影=π-2;再利用勾股定理计算出BD=2
| 3 |
| 3 |
| 3 |
| ||
| 2 |
3
| ||||
| 2 |
| ||
| 3 |
| ||||
| 2 |
| 2 |
解答:解:(1)∵OC⊥DE,
∴DC=EC=
DE=
×2
=
,
∵弦DE垂直平分半径OA,
∴OC=
OA=
OE,
在Rt△OCE中,∵OE=2OC,
∴∠E=30°,
∴OC=
CE=1,
∴OE=2,
即⊙O的半径为2;
(2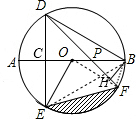 )连结OF,BF,BE,作BH⊥DF于H,如图,
)连结OF,BF,BE,作BH⊥DF于H,如图,
∵∠DPA=45°,
∴∠DDC=45°,
∴∠EOF=2∠EPF=90°,△PCD为等腰直角三角形,
∴图中阴影部分的面积=S扇形EOF-S△OEF
=
-
•2•2
=π-2;
∵BC=AB-AC=4-1=3,
而DC=
,
∴BD=
=2
,
∵BC垂直平分DE,
∴BD=BE=2
,
∵BD=DE=BE,
∴△BED为等边三角形,
∴∠BED=60°,
∴∠BFD=∠BED=60°,
∵△PCD为等腰直角三角形,
∴PC=DC=
,
∴OP=PC-OC=
-1,
∴PB=2-(
-1)=3-
,
在Rt△PBH中,∠BPH=∠DPC=45°,
∴BH=PH=
PB=
,
在Rt△BHF中,∠HBF=30°,
∴HF=
BH=
•
=
,
∴PF=PH+HF=
+
=
,
∴S△PBF=
•
•
=
.
∴DC=EC=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
∵弦DE垂直平分半径OA,
∴OC=
| 1 |
| 2 |
| 1 |
| 2 |
在Rt△OCE中,∵OE=2OC,
∴∠E=30°,
∴OC=
| ||
| 3 |
∴OE=2,
即⊙O的半径为2;
(2
 )连结OF,BF,BE,作BH⊥DF于H,如图,
)连结OF,BF,BE,作BH⊥DF于H,如图,∵∠DPA=45°,
∴∠DDC=45°,
∴∠EOF=2∠EPF=90°,△PCD为等腰直角三角形,
∴图中阴影部分的面积=S扇形EOF-S△OEF
=
| 90•π•22 |
| 360 |
| 1 |
| 2 |
=π-2;
∵BC=AB-AC=4-1=3,
而DC=
| 3 |
∴BD=
| DC2+BC2 |
| 3 |
∵BC垂直平分DE,
∴BD=BE=2
| 3 |
∵BD=DE=BE,
∴△BED为等边三角形,
∴∠BED=60°,
∴∠BFD=∠BED=60°,
∵△PCD为等腰直角三角形,
∴PC=DC=
| 3 |
∴OP=PC-OC=
| 3 |
∴PB=2-(
| 3 |
| 3 |
在Rt△PBH中,∠BPH=∠DPC=45°,
∴BH=PH=
| ||
| 2 |
3
| ||||
| 2 |
在Rt△BHF中,∠HBF=30°,
∴HF=
| ||
| 3 |
| ||
| 3 |
3
| ||||
| 2 |
| ||||
| 2 |
∴PF=PH+HF=
3
| ||||
| 2 |
| ||||
| 2 |
| 2 |
∴S△PBF=
| 1 |
| 2 |
| 2 |
3
| ||||
| 2 |
3-
| ||
| 2 |
点评:本题考查了垂径定理:平分弦的直径平分这条弦,并且平分弦所对的两条弧.也考查了扇形的面积公式、圆周角定理和含30度的直角三角形三边的关系.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目