题目内容
已知四边形ABCD,∠B+∠D=180°,∠BCD=120°,BC=CD,点M、N分别在直线AB、AD上,∠MCN=60°,现将∠MCN绕点C旋转.
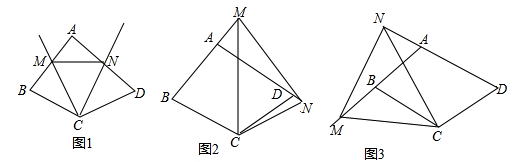
(1)如图1,当点M在AB上,点N在AD上时,则线段BM、DN、MN之间的数量关系为 ;
(2)如图2,点M在BA的延长线上,点N在AD的延长线上时,则线段BN、DM、MN之间的数量关系为 ;
(3)如图3,点M在AB的延长线上,点N在DA的延长线时,则线段BM、DN、MN之间的数量关系为 .

(1)如图1,当点M在AB上,点N在AD上时,则线段BM、DN、MN之间的数量关系为
(2)如图2,点M在BA的延长线上,点N在AD的延长线上时,则线段BN、DM、MN之间的数量关系为
(3)如图3,点M在AB的延长线上,点N在DA的延长线时,则线段BM、DN、MN之间的数量关系为
考点:全等三角形的判定与性质
专题:
分析:(1)在DN的延长线上截取DM1=BM,连接CM1.可证△DCM≌△CDM1,即可得CM=CM1,∠MCB=∠M1CD,M1C=BM,易证得∠M1CN=∠MCN=60°,则可证得△MCN≌△M1CN,然后由全等三角形的性质,即可得BM+NC=MN.
(2)首先在BN上截取BM1=DM,连接CM1,可证△DCM≌△BCM1,即可得DM=DM1,DM=BM1,∠M1CB=∠MCD,然后证得∠M1CN=∠MCN=60°,易证得△MCN≌△M1CN,则可得MN+DM=BN.
(3))首先在DN上截取DM1=BM,连接CM1,可证CBM≌△CDM1,即可得CM=CM1,∠MCB=∠M1CD,BM=DM1,然后证得∠M1CN=∠MCN=60°,易证得△MCN≌△M1CN,则可得ND-BM=MN.
(2)首先在BN上截取BM1=DM,连接CM1,可证△DCM≌△BCM1,即可得DM=DM1,DM=BM1,∠M1CB=∠MCD,然后证得∠M1CN=∠MCN=60°,易证得△MCN≌△M1CN,则可得MN+DM=BN.
(3))首先在DN上截取DM1=BM,连接CM1,可证CBM≌△CDM1,即可得CM=CM1,∠MCB=∠M1CD,BM=DM1,然后证得∠M1CN=∠MCN=60°,易证得△MCN≌△M1CN,则可得ND-BM=MN.
解答:(1)答:如图1,BM、NC、MN之间的数量关系 BM+NC=MN.

证明:在DN的反向延长线上截取DM1=BM,连接CM1.
∵∠B+∠D=180°,∠CDN+∠CDM=180°,
∴∠B=∠CDM,
在△BCM与△DCM1中,
,
∴△BCM≌△DCM1(SAS),
∴CM=CM1,∠MCB=∠M1CD,M1C=BM,
∵∠MCN=60°,∠BCD=120°,
∴∠M1CN=∠MCN=60°,
∴△MCN≌△M1CN,
∴MN=M1N=M1D+ND=BM+ND,
即MN=BM+ND.
(2)MN+DN=BM;
证明:如图2,在BM上截取BN1=DN,连接CN1.

可证△DCN≌△BCN1,
∴CN=CN1,DN=BN1,∠N1CB=∠NCD,
∵∠MCN=60°,∠BCD=120°,
∴∠N1CM=∠MCN=60°,
在△MCN与△MCN1中,
,
∴△MCN≌△MCN1(SAS),
∴MN=MN1,
∴MN+DN=BM.
(3)ND-BM=MN;
证明:如图3,在DN上截取DM1=BM,连接CM1.

可证△CBM≌△CDM1,
∴CM=CM1,∠MCB=∠M1CD,BM=DM1,
∵∠MCN=60°,∠BCD=120°,
∴∠M1CN=∠MCN=60°,
在△NCM1和△NCM中
,
∴△NCM1≌△NCM(SAS),
∴MN=M1N,
∴ND-BM=MN.

证明:在DN的反向延长线上截取DM1=BM,连接CM1.
∵∠B+∠D=180°,∠CDN+∠CDM=180°,
∴∠B=∠CDM,
在△BCM与△DCM1中,
|
∴△BCM≌△DCM1(SAS),
∴CM=CM1,∠MCB=∠M1CD,M1C=BM,
∵∠MCN=60°,∠BCD=120°,
∴∠M1CN=∠MCN=60°,
∴△MCN≌△M1CN,
∴MN=M1N=M1D+ND=BM+ND,
即MN=BM+ND.
(2)MN+DN=BM;
证明:如图2,在BM上截取BN1=DN,连接CN1.

可证△DCN≌△BCN1,
∴CN=CN1,DN=BN1,∠N1CB=∠NCD,
∵∠MCN=60°,∠BCD=120°,
∴∠N1CM=∠MCN=60°,
在△MCN与△MCN1中,
|
∴△MCN≌△MCN1(SAS),
∴MN=MN1,
∴MN+DN=BM.
(3)ND-BM=MN;
证明:如图3,在DN上截取DM1=BM,连接CM1.

可证△CBM≌△CDM1,
∴CM=CM1,∠MCB=∠M1CD,BM=DM1,
∵∠MCN=60°,∠BCD=120°,
∴∠M1CN=∠MCN=60°,
在△NCM1和△NCM中
|
∴△NCM1≌△NCM(SAS),
∴MN=M1N,
∴ND-BM=MN.
点评:此题考查了等边三角形,直角三角形,等腰三角形的性质以及全等三角形的判定与性质等知识.此题综合性很强,难度较大,解题的关键是注意数形结合思想的应用与辅助线的作法.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
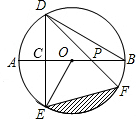 如图,AB是⊙O的直径,弦DE垂直平分半径OA,C为垂足,弦DF与半径OB相交于点P,连接EF、EO.若DE=2
如图,AB是⊙O的直径,弦DE垂直平分半径OA,C为垂足,弦DF与半径OB相交于点P,连接EF、EO.若DE=2
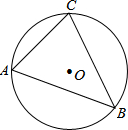 如图,圆O是△ABC的外接圆,圆O的半径为6,∠ABC=45°,求AC的长.
如图,圆O是△ABC的外接圆,圆O的半径为6,∠ABC=45°,求AC的长.