题目内容
10.菱形ABCD的两条对角线AC=6,BD=4,则$sin\frac{A}{2}$的值是( )| A. | $\frac{5}{13}$ | B. | $\frac{5}{12}$ | C. | $\frac{{3\sqrt{13}}}{13}$ | D. | $\frac{{2\sqrt{13}}}{13}$ |
分析 由菱形的性质得出OA=$\frac{1}{2}$AC=3,OB=$\frac{1}{2}$BD=2,AC⊥BD,∠BAC=∠DAB=$\frac{1}{2}$∠BAD,由勾股定理求出AB,由三角函数即可得出结果.
解答 解:如图所示: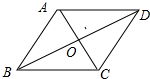
∵四边形ABCD是菱形,
∴OA=$\frac{1}{2}$AC=3,OB=$\frac{1}{2}$BD=2,AC⊥BD,∠BAC=∠DAB=$\frac{1}{2}$∠BAD,
∴∠AOB=90°,
∴AB=$\sqrt{O{A}^{2}+O{B}^{2}}$=$\sqrt{{3}^{2}+{2}^{2}}$=$\sqrt{13}$,
∴sin$\frac{∠BAD}{2}$=$\frac{OB}{AB}$=$\frac{2}{\sqrt{13}}$=$\frac{2\sqrt{13}}{13}$;
故选:D.
点评 本题考查了菱形的性质、勾股定理、三角函数;熟练掌握菱形的性质,并能进行推理计算是解决问题的关键.

练习册系列答案
相关题目
20.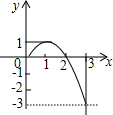 已知二次函数y=ax2+bx+c(a≠0)(0≤x≤3)的图象如图所示,则该函数在所给自变量取值范围内,下列说法正确的是( )
已知二次函数y=ax2+bx+c(a≠0)(0≤x≤3)的图象如图所示,则该函数在所给自变量取值范围内,下列说法正确的是( )
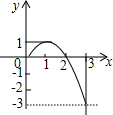 已知二次函数y=ax2+bx+c(a≠0)(0≤x≤3)的图象如图所示,则该函数在所给自变量取值范围内,下列说法正确的是( )
已知二次函数y=ax2+bx+c(a≠0)(0≤x≤3)的图象如图所示,则该函数在所给自变量取值范围内,下列说法正确的是( )| A. | 有最大值1,没有最小值 | B. | 有最大值3,有最小值-3 | ||
| C. | 有最大值1,有最小值-3 | D. | 有最大值3,有最小值1 |
19.点A的坐标为A(2,-4),若点A绕原点逆时针旋转270°后的坐标为( )
| A. | (-4,2) | B. | (-4,-2) | C. | (4,-2) | D. | (4,2) |
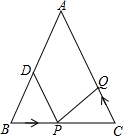 如图所示,已知△ABC中,AB=AC=10厘米,BC=8厘米,点D为AB的中点.
如图所示,已知△ABC中,AB=AC=10厘米,BC=8厘米,点D为AB的中点.  如图,直线AB、CD相交于点O,OB平分∠DOE,若∠DOE=60°,则∠BOE的度数是30°.∠AOC的度数是30°.
如图,直线AB、CD相交于点O,OB平分∠DOE,若∠DOE=60°,则∠BOE的度数是30°.∠AOC的度数是30°.