题目内容
18.已知关于x的不等式组$\left\{\begin{array}{l}x-a≥0\\ 2-2x>-1\end{array}\right.$的整数解共有5个,求a的取值范围-4<a≤-3.分析 先分别解两个不等式得到不等式组的解集为a≤x<$\frac{3}{2}$,则可确定不等式组的整数解为1,0,-1,-2,-3,于是可得到a的范围.
解答 解:$\left\{\begin{array}{l}{x-a≥0①}\\{2-2x>-1②}\end{array}\right.$,
解①得x≥a,
解②得x<$\frac{3}{2}$,
所以不等式组的解集为a≤x<$\frac{3}{2}$,
而不等式组的整数解共有5个,即1,0,-1,-2,-3,
所以-4<a≤-3.
故答案为-4<a≤-3.
点评 本题考查了一元一次不等式组的整数解:已知解集(整数解)求字母的取值.一般思路为:先把题目中除未知数外的字母当做常数看待解不等式组或方程组等,然后再根据题目中对结果的限制的条件得到有关字母的代数式,最后解代数式即可得到答案.

练习册系列答案
相关题目
8.下列各式计算正确的是( )
| A. | $\sqrt{(-9)(-4)}=\sqrt{-9}•\sqrt{-4}=(-3)(-2)=6$ | B. | $\sqrt{8}-\sqrt{2}=\sqrt{2}$ | ||
| C. | $\sqrt{{3^2}+{4^2}}=3+4=7$ | D. | $\frac{{6-\sqrt{2}}}{{\sqrt{2}}}=3\sqrt{2}$ |
9.下列各式中与x3n+1相等的是( )
| A. | (x3)n+1 | B. | (xn+1)3 | C. | x3•xn•x | D. | x•x3n |
6.化简:$\frac{4}{{{a^2}-4}}+\frac{1}{2-a}$的结果是( )
| A. | 2-a | B. | -2-a | C. | $\frac{1}{2-a}$ | D. | $-\frac{1}{2+a}$ |
10.菱形ABCD的两条对角线AC=6,BD=4,则$sin\frac{A}{2}$的值是( )
| A. | $\frac{5}{13}$ | B. | $\frac{5}{12}$ | C. | $\frac{{3\sqrt{13}}}{13}$ | D. | $\frac{{2\sqrt{13}}}{13}$ |
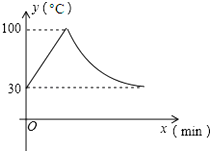 教室里的饮水机接通电源就进入加热程序,水温每分钟上升10℃,加热到100℃时自动关机,水温开始下降,此时水温(℃)与时间(min)成反比例关系.若室温恒定为30℃,当水温降至30℃时,又启动第二轮加热程序.某轮加热过程中水温y(℃)和时间x(min)的关系如图所示.
教室里的饮水机接通电源就进入加热程序,水温每分钟上升10℃,加热到100℃时自动关机,水温开始下降,此时水温(℃)与时间(min)成反比例关系.若室温恒定为30℃,当水温降至30℃时,又启动第二轮加热程序.某轮加热过程中水温y(℃)和时间x(min)的关系如图所示.