题目内容
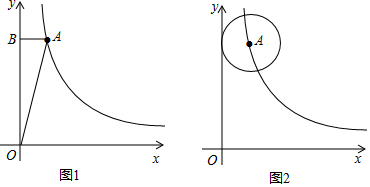
2.在△ABC中,AB=AC=4,∠BAC=30°,以AB为斜边作等腰直角△ABD.请画出图形,并直接写出△BCD的面积.分析 根据题意画出图形,利用勾股定理以及直角三角形的性质求出BC的长,分两种情况,求出BC边上的高,进而求出答案.
解答 解: 分两种情况:
分两种情况:
①如图1所示:作BM⊥AC与M,
∵∠BAC=30°,
∴BM=$\frac{1}{2}$AB=2,
∴AM=$\sqrt{3}$BM=2$\sqrt{3}$,
∴CM=AC-AM=4-2$\sqrt{3}$,
在Rt△BCM中,由勾股定理得:BC=$\sqrt{B{M}^{2}+C{M}^{2}}$=$\sqrt{{2}^{2}+(4-2\sqrt{3})^{2}}$=2$\sqrt{6}$-2$\sqrt{2}$,
作DE⊥BC于E,∵AB=AC=4,∠BAC=30°,
∴∠ABC=75°,
∵△ABD是等腰直角三角形,
∴∠ABD=45°,BD=$\frac{\sqrt{2}}{2}$AB=2$\sqrt{2}$,
∴∠DBE=180°-45°-75°=60°,
∴∠BDE=30°,
∴BE=$\frac{1}{2}$BD=$\sqrt{2}$,
∴DE=$\sqrt{3}$BE=$\sqrt{6}$,
∴△BCD的面积=$\frac{1}{2}$BC•DE=$\frac{1}{2}$(2$\sqrt{6}$-2$\sqrt{2}$)×$\sqrt{6}$=6-2$\sqrt{3}$;
②如图2所示:作DF⊥BC于F,
∵∠DBF=75°-45°=30°,
∴DF=$\frac{1}{2}$BD=$\sqrt{2}$,
∴△BCD的面积=$\frac{1}{2}$BC•DF=$\frac{1}{2}$(2$\sqrt{6}$-2$\sqrt{2}$)×$\sqrt{2}$=2$\sqrt{3}$-2.
点评 此题主要考查了勾股定理、等腰三角形的性质、三角形内角和定理、等腰直角三角形的性质、含30°角的直角三角形的性质等知识,得出BC的长是解题关键,注意分类讨论.

 阅读快车系列答案
阅读快车系列答案| 加数的个数n | S |
| 1 | 2=1×2 |
| 2 | 2+4=6=2×3 |
| 3 | 2+4+6=15=3×4 |
| 4 | 2+4+6+8=20=4×5 |
| 5 | 2+4+6+8+10=30=5×6 |
(2)如下数表是由从1开始的连续自然数组成,观察规律:
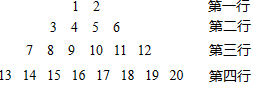
①第n行的第一个数可用含n的式子表示为:n2-n+1;
②如果某行的第一个数为157,求其所在的行数.
| A. | m≤2 | B. | m<2 | C. | m≤2且m≠1 | D. | m<2且m≠1 |
 已知:正方体展开图(如图所示)相对面上的数值相等,那么x的值等于( )
已知:正方体展开图(如图所示)相对面上的数值相等,那么x的值等于( )| A. | -1 | B. | a-2 | C. | -1或2 | D. | 1或-2 |
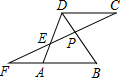 如图,点P是菱形ABCD对角线BD上一点,连接CP并延长,交AD于点E,交BA的延长线于点F,则线段PC、PE、PF之间存在的数量关系是( )
如图,点P是菱形ABCD对角线BD上一点,连接CP并延长,交AD于点E,交BA的延长线于点F,则线段PC、PE、PF之间存在的数量关系是( )| A. | 2PC=PE+PF | B. | 2PC=PE•PF | C. | PC2=PE•PF | D. | PC2=$\frac{PF}{PE}$ |