题目内容
3．数学复习课上，老师出示4张背面完全相同的卡片，卡片正面写有方程如下，若把这4张卡片背面朝上前打乱顺序，求下列事件的概率：（1）随机抽取一张，恰好卡片上是一元一次方程；
（2）随机抽取两张，恰好卡片上都是只有一个根的方程．
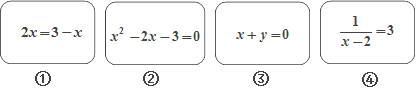
分析 （1）先根据一元一次方程的定义找出一元一次方程，再根据概率公式即可得出结论；
（2）画树状图列出所有等可能结果，再在所有结果中找到只有一个根的方程，由概率公式计算可得．
解答 解：（1）在四个方程中，是一元一次方程的值只有①，
∴随机抽取一张，恰好卡片上是一元一次方程的概率为$\frac{1}{4}$；
（2）画树状图如下：
∵方程①的根为x=1、方程②的根为x=-1或x=3、方程③有无数组解、方程④的根为x=2$\frac{1}{3}$，
∴在所有12种等可能结果中，恰好都是只有一个根的方程有①④、④①这2种结果，
∴随机抽取两张，恰好卡片上都是只有一个根的方程的概率为$\frac{2}{12}$=$\frac{1}{6}$．
点评 此题考查了列表法或树状图法求概率．用到的知识点为：概率=所求情况数与总情况数之比．
练习册系列答案
相关题目
13．从2开始，连续的偶数相加，它们和的情况如表：
（1）根据表中的规律猜想：用n的式子表示S的公式为：S=2+4+6+8+…+2n=n（n+1）；
（2）如下数表是由从1开始的连续自然数组成，观察规律：
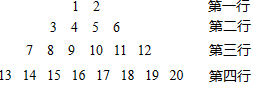
①第n行的第一个数可用含n的式子表示为：n2-n+1；
②如果某行的第一个数为157，求其所在的行数．
| 加数的个数n | S |
| 1 | 2=1×2 |
| 2 | 2+4=6=2×3 |
| 3 | 2+4+6=15=3×4 |
| 4 | 2+4+6+8=20=4×5 |
| 5 | 2+4+6+8+10=30=5×6 |
（2）如下数表是由从1开始的连续自然数组成，观察规律：
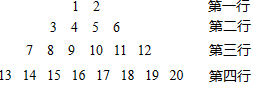
①第n行的第一个数可用含n的式子表示为：n2-n+1；
②如果某行的第一个数为157，求其所在的行数．
14．
已知：正方体展开图（如图所示）相对面上的数值相等，那么x的值等于（ ）
已知：正方体展开图（如图所示）相对面上的数值相等，那么x的值等于（ ）| A． | -1 | B． | a-2 | C． | -1或2 | D． | 1或-2 |
11．
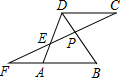如图，点P是菱形ABCD对角线BD上一点，连接CP并延长，交AD于点E，交BA的延长线于点F，则线段PC、PE、PF之间存在的数量关系是（ ）
如图，点P是菱形ABCD对角线BD上一点，连接CP并延长，交AD于点E，交BA的延长线于点F，则线段PC、PE、PF之间存在的数量关系是（ ）| A． | 2PC=PE+PF | B． | 2PC=PE•PF | C． | PC2=PE•PF | D． | PC2=$\frac{PF}{PE}$ |
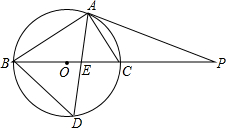如图，已知⊙O中，PA切⊙O于A，PB过圆心且与圆交于点C，D为$\widehat{BC}$中点，AD交BC于E，若AB=8，tan∠ABC=$\frac{3}{4}$．