题目内容
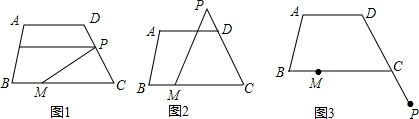
如图，∠1+∠C=100°，∠2+∠B=100°，AB与CD平行吗？说明你的理由．考点：平行线的判定
专题：
分析：AB与CD平行，理由：由∠1+∠C=100°，∠2+∠B=100°，根据三角形内角和定理可求∠D=80°，∠A=80°，进而得到：∠A=∠D，然后根据内错角相等，两直线平行即可判定AB与CD平行．
解答：
解：AB与CD平行．
理由：
∵∠1+∠C=100°，∠2+∠B=100°，且∠1+∠C+∠D=180°，∠2+∠B+∠A=180°，
∴∠D=80°，∠A=80°，
即：∠A=∠D，
∴AB∥CD．
理由：
∵∠1+∠C=100°，∠2+∠B=100°，且∠1+∠C+∠D=180°，∠2+∠B+∠A=180°，
∴∠D=80°，∠A=80°，
即：∠A=∠D，
∴AB∥CD．
点评：此题考查了平行线的判定，利用角判断两直线平行的方法有：同位角相等，两直线平行；内错角相等，两直线平行；同旁内角互补，两直线平行．
练习册系列答案
阅读快车系列答案
相关题目
如图所示，OA=OB，∠O=60°，AC=OD，∠OAD=25°．求∠ACB的度数．
如图所示，在Rt△ABC中，∠C=90°，AD为∠CAB的平分线，CD=3厘米，则点D到AB的距离为（ ）| A、3厘米 | B、6厘米 |
| C、9厘米 | D、不能确定 |
如果AD是△ABC的中线，那么下列结论一定成立的有（ ）
①BD=CD；②AB=AC；③S△ABD=
S△ABC．
①BD=CD；②AB=AC；③S△ABD=
| 1 |
| 2 |
| A、3个 | B、2个 | C、1个 | D、0个 |
下列说法中不正确的是（ ）
| A、全等三角形的周长相等 |
| B、全等三角形的面积相等 |
| C、全等三角形一定能够重合 |
| D、全等三角形一定关于某直线对称 |
下列运算正确的是（ ）
| A、a3•a3=2a3 |
| B、a3+a3=a6 |
| C、（-2a2）3=-8a6 |
| D、a6÷a3=a2 |