题目内容
1.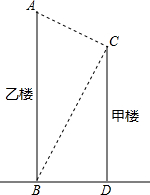 如图,在一幢高CD=15m的甲楼顶端C处,测得乙楼底部B的俯角为63°,乙楼顶端A的仰角为25°.求:
如图,在一幢高CD=15m的甲楼顶端C处,测得乙楼底部B的俯角为63°,乙楼顶端A的仰角为25°.求:(1)两楼的水平距离BD;
(2)乙楼的高度AB.
分析 作CE⊥AB于E,则∠AEC=90°,根据题意得:BE=CD=15m,CE=BD,∠ACE=25°,∠CBD=63°;
(1)由三角函数求出BD即可;
(2)由三角函数求出AE,即可得出AB.
解答 解:作CE⊥AB于E,如图所示: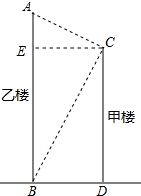
则∠AEC=90°,
根据题意得:BE=CD=15m,CE=BD,∠ACE=25°,∠CBD=63°,
(1)在Rt△BCD中,∵tan∠CBD=$\frac{CD}{BD}$,
∴BD=$\frac{CD}{tan63°}$=$\frac{15}{2.0503}$≈7.316(米).
答:两楼的水平距离BD约为7.316米;
(2)由(1)得:CE=BD=7.316米,
在Rt△ACE中,AE=CE•tan25°=7.316×0.4877≈3.568(米),
∴AB=AE+BE=3.568+15=18.568(米).
答:乙楼的高度AB约为18.568米.
点评 本题考查了解直角三角形的应用,解答本题的关键是构造直角三角形,利用三角函数的知识求解相关线段的长度.

练习册系列答案
相关题目
 如图,∠AOB是直角,OD平分∠BOC,OE平分∠AOC,求∠EOD的度数.
如图,∠AOB是直角,OD平分∠BOC,OE平分∠AOC,求∠EOD的度数.
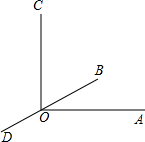 如图,已知∠AOC=90°,直线BD过点O,∠COD=115°15′,则∠AOB=25°15′.
如图,已知∠AOC=90°,直线BD过点O,∠COD=115°15′,则∠AOB=25°15′.