题目内容
18.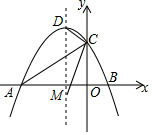 如图,抛物线y=-$\frac{1}{2}$x2-$\frac{3}{2}$x+2与x轴交于A、B两点,与y轴交于C点,D为抛物线的顶点,M为抛物线对称轴上一点,当∠ACD=∠BCM时,求M点坐标.
如图,抛物线y=-$\frac{1}{2}$x2-$\frac{3}{2}$x+2与x轴交于A、B两点,与y轴交于C点,D为抛物线的顶点,M为抛物线对称轴上一点,当∠ACD=∠BCM时,求M点坐标.
分析 首先证明∠ACB=90°,过C作CM⊥CD交x轴于M,由∠DCM=∠ACB=90°,推出∠DCA=∠MCB,求出直线CM的解析式即可解决问题.
解答 解:对于抛物线y=-$\frac{1}{2}$x2-$\frac{3}{2}$x+2,
令x=0,得y=2,∴ C(0,2),
C(0,2),
令y=0得-$\frac{1}{2}$x2-$\frac{3}{2}$x+2=0,解得x=-4或1,
∴A(-4,0),B(1,0),
∴AB=5.AC=2$\sqrt{5}$,BC=$\sqrt{5}$,
∴AB2=AC2+BC2,
∴∠ACB=90°,
过C作CM⊥CD交x轴于M,
∵∠DCM=∠ACB=90°,
∴∠DCA=∠MCB,
∵D(-$\frac{3}{2}$,$\frac{25}{8}$),
∴直线CD的解析式为y=-$\frac{3}{4}$x+2,
∵CM⊥CD,
∴直线CM的解析式为y=$\frac{4}{3}$x+2,
令y=0,得x=-$\frac{3}{2}$,
∴点M坐标(-$\frac{3}{2}$,0).
点评 本题考查抛物线与x轴的交点、勾股定理逆定理、两条直线垂直k的乘积为-1等知识,解题的关键是发现∠ACB=90°,求出直线CM是关键,属于中考常考题型.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
 小明想把一长为25cm,宽为20cm的长方形硬纸片做成一个无盖的长方体盒子,于是在长方形纸片的四个角各剪去一个相同的小正方形.
小明想把一长为25cm,宽为20cm的长方形硬纸片做成一个无盖的长方体盒子,于是在长方形纸片的四个角各剪去一个相同的小正方形.